题目内容
【题目】已知 
=（3，4）， 
是单位向量．
（1）若 ∥ ，求 ；
（2）若 ⊥ ，求 ．
【答案】
（1）解：因为 
=（3，4）， 
是单位向量，设 =（xy）x2+y2=1①；
当 ∥ 时，3y﹣4x=0②，
由①②组成方程组，解得 
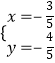或 
，
∴ =（ 
， 
）或（﹣ ，﹣ ）
（2）解：当 ⊥ 时，3x+4y=0③，
由①③组成方程组，解得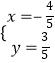 
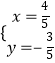或 
；
∴ =（﹣ ， ）或（ ，﹣ ）
【解析】根据平面向量的坐标运算，利用单位向量的定义和向量的共线定理，列出方程组求出（1）中 的坐标；利用两向量垂直时数量积为0，列出方程组求出（2）中 的坐标．
【考点精析】关于本题考查的平面向量的坐标运算，需要了解坐标运算：设
，
则
;
;设
，则
才能得出正确答案．
练习册系列答案
相关题目
【题目】为研究男女同学空间想象能力的差异，孙老师从高一年级随机选取了20名男生、20名女生，进行空间图形识别测试，得到成绩茎叶图如下，假定成绩大于等于80分的同学为“空间想象能力突出”，低于80分的同学为“空间想象能力正常”.
（1）完成下面
列联表，并判断是否有
的把握认为“空间想象能力突出”与性别有关；
空间想象能力突出 | 空间想象能力正常 | 合计 | |
男生 | |||
女生 | |||
合计 |
（2）从“空间想象能力突出”的同学中随机选取男生2名、女生2名，记其中成绩超过90分的人数为
，求随机变量
的分布列和数学期望.
下面公式及临界值表仅供参考： 
| 0.100 | 0.050 | 0.010 | |
| 2.706 | 3.841 | 6.635 |
