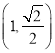Question

【题目】在△ABC中，点D，E分别是边AB，AC上的一点，且满足AD= AB，AE= AC，若BE⊥CD，则cosA的最小值是 ．

Answer 1

【答案】
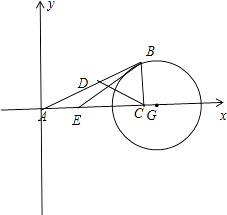
【解析】解：如图所示，不妨设C（3，0），B（x，y），A（0，0）．
∵AD= AB，AE= AC，∴E（1，0），D ．
∵BE⊥CD，
∴ =（1﹣x，﹣y） = ﹣ =0，
化为： +y2= ．圆心G ，半径r= ．
设圆的切线方程为y=kx（取k＞0）．
则 = ，化为k2= ，解得k= ．
当AB与⊙G相切时，∠A最大，cosA最小．
此时tanA= ，
∴cosA= = ．
∴cosA的最小值为 ．
所以答案是： ．

【考点精析】根据题目的已知条件，利用正弦定理的定义的相关知识可以得到问题的答案，需要掌握正弦定理:．