题目内容
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为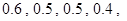 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.
(1)求同一工作日至少3人需使用设备的概率;
(2)X表示同一工作日需使用设备的人数,求X的数学期望.
(1)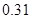 ;(2)2.
;(2)2.
解析试题分析:(1)首先用字母表示有关的事件,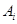 表示事件:同一工作日乙、丙恰有
表示事件:同一工作日乙、丙恰有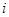 人需使用设备,
人需使用设备,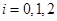 ;
;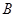 表示事件:甲需使用设备;
表示事件:甲需使用设备;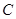 表示事件:丁需使用设备;
表示事件:丁需使用设备;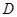 表示事件:同一工作日至少3人需使用设备.将
表示事件:同一工作日至少3人需使用设备.将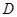 分解为互斥事件的和:
分解为互斥事件的和: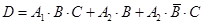 ,再利用互斥事件的概率加法公式计算
,再利用互斥事件的概率加法公式计算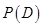 ;(2)
;(2)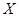 的可能取值为0,1,2,3,4.先用分解策略求分别
的可能取值为0,1,2,3,4.先用分解策略求分别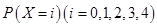 ,最后利用离散型随机变量数学期望公式求
,最后利用离散型随机变量数学期望公式求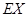 的值.
的值.
试题解析:记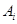 表示事件:同一工作日乙、丙恰有
表示事件:同一工作日乙、丙恰有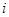 人需使用设备,
人需使用设备,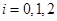 ;
;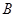 表示事件:甲需使用设备;
表示事件:甲需使用设备;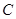 表示事件:丁需使用设备;
表示事件:丁需使用设备;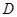 表示事件:同一工作日至少3人需使用设备.
表示事件:同一工作日至少3人需使用设备.
(1)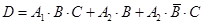 ,
,
又
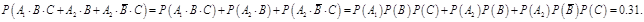 (2)
(2)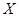 的可能取值为0,1,2,3,4.
的可能取值为0,1,2,3,4.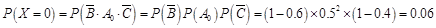 ,
,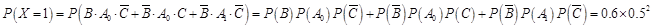
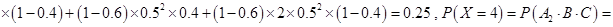
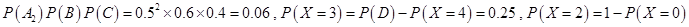
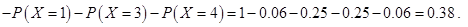 ∴数学期望
∴数学期望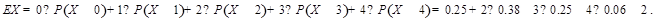 考点:1.相互独立事件的概率计算;2.离散型随机变量的数学期望的计算.
考点:1.相互独立事件的概率计算;2.离散型随机变量的数学期望的计算.

练习册系列答案
相关题目
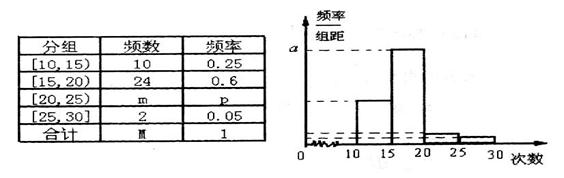
某学校组织了一次安全知识竞赛,现随机抽取20名学生的测试成绩,如下表所示(不低于90分的测试成绩称为“优秀成绩”):
| 79 | 90 | 82 | 80 | 84 | 95 | 79 | 86 | 89 | 91 |
| 97 | 86 | 79 | 78 | 86 | 77 | 87 | 89 | 83 | 85 |
(1)若从这20人中随机选取3人,求至多有1人是“优秀成绩”的概率;
(2)以这20人的样本数据来估计整个学校的总体数据,若从该校全体学生中(人数很多)任选3人,记
 表示抽到“优秀成绩”学生的人数,求
表示抽到“优秀成绩”学生的人数,求 的分布列及数学期望.
的分布列及数学期望. 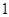 的球
的球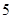 个,编号为
个,编号为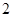 的球
的球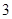 个,这些球的大小完全一样。
个,这些球的大小完全一样。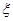 为这三个球的编号之和,求随机变量
为这三个球的编号之和,求随机变量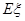 .
. .
.
 ,第二次出现的点数为
,第二次出现的点数为 .
.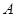 为“
为“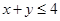 ”,求
”,求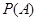 ;
;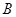 为“
为“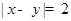 ”,求
”,求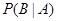 .
.
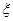 ,求
,求 .
.