题目内容
某学校组织了一次安全知识竞赛,现随机抽取20名学生的测试成绩,如下表所示(不低于90分的测试成绩称为“优秀成绩”):
| 79 | 90 | 82 | 80 | 84 | 95 | 79 | 86 | 89 | 91 |
| 97 | 86 | 79 | 78 | 86 | 77 | 87 | 89 | 83 | 85 |
(1)若从这20人中随机选取3人,求至多有1人是“优秀成绩”的概率;
(2)以这20人的样本数据来估计整个学校的总体数据,若从该校全体学生中(人数很多)任选3人,记
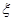 表示抽到“优秀成绩”学生的人数,求
表示抽到“优秀成绩”学生的人数,求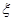 的分布列及数学期望.
的分布列及数学期望.
(1)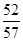 (2)详见解析.
(2)详见解析.
解析试题分析:(1)从抽取的20名学生的测试成绩中统计出成绩优秀的学生共4人,从20人中随机选取3人,有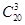 种不同结果,其中至多一人成绩优秀的有
种不同结果,其中至多一人成绩优秀的有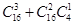 种,可用古典概型求解概率值.
种,可用古典概型求解概率值.
(2)由样本估计总体可知抽到“优秀成绩”学生的概率 ,由于学生人数很多,因此任选3人可看作3次独立重复试验,即
,由于学生人数很多,因此任选3人可看作3次独立重复试验,即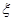 服从
服从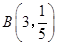
解:(1)由表知:“优秀成绩”为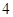 人. 1分
人. 1分
设随机选取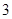 人,至多有
人,至多有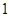 人是“优秀成绩”为事件
人是“优秀成绩”为事件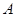 ,则
,则 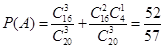 . 5分
. 5分
(2)由样本估计总体可知抽到“优秀成绩”学生的概率 . 6分
. 6分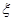 可取
可取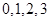 7分
7分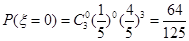 ;
;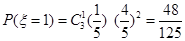 ;
;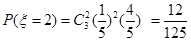 ;
;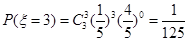 .
.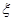 的分布列:
的分布列: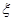
0 1 2 3 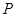
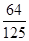


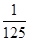
11分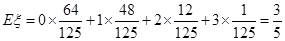 . 12分
. 12分
或 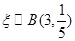 ,
, 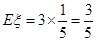 . 12分
. 12分
考点:1、古典概型;2、独立重复试验;3、二项分布.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 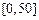 | 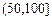 | 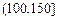 | 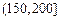 | 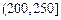 | 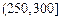 | 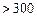 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为ω。在区间[0,100]对企业没有造成经济损失;在区间
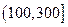 对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;(1)试写出是S(ω)的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
|
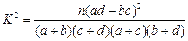
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
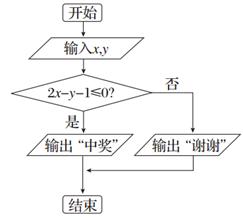
某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2 100 | 1 027 | 376 | 697 |
乙的频数统计表(部分)
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2 100 | 1 051 | 696 | 353 |
当n=2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大;
(3)将按程序框图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.
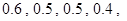 各人是否需使用设备相互独立.
各人是否需使用设备相互独立. ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验.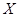 的概率分布列和期望.
的概率分布列和期望.  ,V(η)=
,V(η)= ,求a∶b∶c.
,求a∶b∶c.