题目内容
【题目】在平面直角坐标系xOy中,已知曲线C1的参数方程为 ![]() (φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4
(φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4 ![]() cosθ.
cosθ.
(1)求C1与C2交点的直角坐标;
(2)已知曲线C3的参数方程为 ![]() (0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
(0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
【答案】
(1)解:曲线C1的参数方程为 ![]() (φ为参数),
(φ为参数),
消去参数可得:x2+(y﹣2)2=4.
曲线C2的极坐标方程为ρ=4 ![]() cosθ,即ρ2=4
cosθ,即ρ2=4 ![]() ρcosθ,
ρcosθ,
化为直角坐标方程:x2+y2=4 ![]() x.
x.
联立 ![]() ,
,
解得 ![]() ,
, ![]() ,
,
∴C1与C2交点的直角坐标分别为:(0,0); ![]() .
.
(2)解:曲线C3的参数方程为 ![]() (0≤α<π,t为参数,且t≠0),
(0≤α<π,t为参数,且t≠0),
![]() 时,可得
时,可得 ![]() ,代入方程:x2+(y﹣2)2=4,解得t=0,t=4.
,代入方程:x2+(y﹣2)2=4,解得t=0,t=4.
代入:x2+y2=4 ![]() x,解得t=0,不满足|PQ|=8,舍去.
x,解得t=0,不满足|PQ|=8,舍去.
![]() 时,消去参数化为普通方程:y=xtanα,设k=tanα.
时,消去参数化为普通方程:y=xtanα,设k=tanα.
联立 ![]() ,解得
,解得 ![]() ,
,  ,
,
可得P(0,0),或P ![]() .
.
联立 ![]() ,解得
,解得 ![]() ,
, 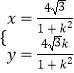 ,
,
可得Q(0,0),或Q ![]() .
.
∵|PQ|=8,∴只能取P ![]() ,Q
,Q ![]() .
.
∴ ![]() +
+ ![]() =82,
=82,
化为: ![]() =0,解得k=﹣
=0,解得k=﹣ ![]() ,
,
∴tanα=﹣ ![]() ,又0≤α<π,解得α=
,又0≤α<π,解得α= ![]()
【解析】(1)曲线C1的参数方程为 ![]() (φ为参数),消去参数可得普通方程.曲线C2的极坐标方程为ρ=4
(φ为参数),消去参数可得普通方程.曲线C2的极坐标方程为ρ=4 ![]() cosθ,即ρ2=4
cosθ,即ρ2=4 ![]() ρcosθ,利用互化公式可得直角坐标方程,联立解出即可得出.(2)曲线C3的参数方程为
ρcosθ,利用互化公式可得直角坐标方程,联立解出即可得出.(2)曲线C3的参数方程为 ![]() (0≤α<π,t为参数,且t≠0),
(0≤α<π,t为参数,且t≠0), ![]() 时,不满足|PQ|=8,舍去.
时,不满足|PQ|=8,舍去. ![]() 时,消去参数化为普通方程:y=xtanα,设k=tanα,即直线l的方程为:y=kx,分别与曲线C1 , C2的方程联立解出交点P,Q的坐标,利用两点之间的距离公式即可得出.
时,消去参数化为普通方程:y=xtanα,设k=tanα,即直线l的方程为:y=kx,分别与曲线C1 , C2的方程联立解出交点P,Q的坐标,利用两点之间的距离公式即可得出.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ) ![]() 在某一个周期内的图象时,列表并填入了部分数据,如表:
在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
f(x)=Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将如表数据补充完整,并直接写出函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位长度,得到函数y=g(x)的图象,求y=g(x)的图象离原点O最近的对称中心.
个单位长度,得到函数y=g(x)的图象,求y=g(x)的图象离原点O最近的对称中心.
(3)求当 ![]() 时,函数y=g(x)的值域.
时,函数y=g(x)的值域.
【题目】抽样调查某大型机器设备使用年限x和该年支出维修费用y(万元),得到数据如表
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
部分数据分析如下 ![]() =25,
=25, ![]() yi=112.3,
yi=112.3, ![]() =90
=90
参考公式:线性回归直线方程为 ![]() ,
, 
(1)求线性回归方程;
(2)由(1)中结论预测第10年所支出的维修费用.