题目内容
【题目】已知函数![]() .
.
(1)求![]() 的极值;
的极值;
(2)证明:![]() 时,
时,![]()
(3)若函数![]() 有且只有三个不同的零点,分别记为
有且只有三个不同的零点,分别记为![]() ,设
,设![]() 且
且![]() 的最大值是
的最大值是![]() ,证明:
,证明:![]()
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)见解析
【解析】
(Ⅰ)先求导数,再根据![]() 讨论导函数零点情况,最后根据导函数零点以及导函数符号变化规律确定极值,(Ⅱ)作差函数
讨论导函数零点情况,最后根据导函数零点以及导函数符号变化规律确定极值,(Ⅱ)作差函数![]() ,先利用导数研究导函数单调性,确定导函数零点,再根据导函数符号确定函数最小值,最后根据基本不等式证得结论,(Ⅲ)先利用导数研究
,先利用导数研究导函数单调性,确定导函数零点,再根据导函数符号确定函数最小值,最后根据基本不等式证得结论,(Ⅲ)先利用导数研究![]() 有两个零点时,其两个零点对应区间,再令
有两个零点时,其两个零点对应区间,再令![]() ,根据条件用
,根据条件用![]() 表示
表示![]() ,利用导数求其最大值,即得结论.
,利用导数求其最大值,即得结论.
(Ⅰ)函数的定义域为![]() .
.
由已知可得![]() .
.
(1)当![]() 时,
时,![]() ,故
,故![]() 在区间
在区间![]() 上单调递增;
上单调递增; ![]() 无极值.
无极值.
(2)当![]() 时,由
时,由![]() ,解得
,解得![]() ;由
;由![]() ,解得
,解得![]() .所以函数
.所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减. ![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(Ⅱ)证明:令![]() ,故只需证明
,故只需证明![]() .
.
因为![]()
所以函数![]() 在
在![]() 上为增函数,且
上为增函数,且![]() ,
,![]() .
.
故![]() 在
在![]() 上有唯一实数根
上有唯一实数根![]() ,且
,且![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
从而当![]() 时,
时,![]() 取得最小值.
取得最小值.
由![]() ,得
,得![]() ,即
,即![]() ,
,
故![]()
![]() ,
,
因为![]() ,所以等于号取不到,即
,所以等于号取不到,即![]()
综上,当![]() 时,
时,![]() 即
即![]() .
.
(Ⅲ)∵ 函数![]() 有且只有三个不同的零点,而
有且只有三个不同的零点,而![]() 是其零点,
是其零点,
∴ 函数![]() 存在两个零点(不等于
存在两个零点(不等于![]() ),即
),即![]() 有两个不等且不等于
有两个不等且不等于![]() 的实数根.
的实数根.
可转化为方程![]() 在区间
在区间![]() 上有两个不等且不等于
上有两个不等且不等于![]() 的实数根,
的实数根,
即函数![]() 的图象与函数
的图象与函数![]() 的图象有两个交点.
的图象有两个交点.
∵![]() ,
,
∴ 由![]() ,解得
,解得![]() ,故
,故![]() 在上单调递增;
在上单调递增;
由![]() ,解得
,解得![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
故函数![]() 的图象与
的图象与![]() 的图象的交点分别在
的图象的交点分别在![]() ,
,![]() 上,
上,
即![]() 的两个根分别在区间
的两个根分别在区间![]() ,
,![]() 上,
上,
∴![]() 的三个不同的零点分别是
的三个不同的零点分别是![]() ,且
,且![]() .
.
令![]() ,则
,则![]() .
.
由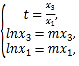 ,解得
,解得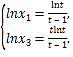 故
故![]() ,
, ![]() .-令
.-令![]() ,则
,则![]() .
.
令![]() ,则
,则![]() .
.
所以![]() 在区间
在区间![]() 上单调递增,即
上单调递增,即![]() .
.
所以![]() ,即
,即![]() 在区间
在区间![]() 上单调递增,
上单调递增,
即![]() ,
,
所以![]() ,即
,即![]() ,
,

【题目】某医院治疗白血病有甲、乙两套方案,现就70名患者治疗后复发的情况进行了统计,得到其等高条形图如图所示(其中采用甲、乙两种治疗方案的患者人数之比为![]() .
.
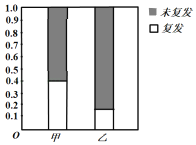
(1)补充完整![]() 列联表中的数据,并判断是否有
列联表中的数据,并判断是否有![]() 把握认为甲乙两套治疗方案对患者白血病复发有影响;
把握认为甲乙两套治疗方案对患者白血病复发有影响;
复发 | 未复发 | 总计 | |
甲方案 | |||
乙方案 | 2 | ||
总计 | 70 |
(2)为改进“甲方案”,按分层抽样组成了由5名患者构成的样本,求随机抽取2名患者恰好是复发患者和未复发患者各1名的概率.
附:
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 |
![]() ,
,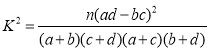 .
.