题目内容
5.已知数列{an}满足a1=1,$\frac{{a}_{n+1}}{{a}_{n}+1}$=$\frac{n+2}{n}$(n∈N*).(1)求a2,a3,a4;
(2)写出数列{an}的通项公式,并证明你的结论.
分析 (1)由已知直接求出a2,a3,a4;
(2)把(1)中求得的数列的前几项变形,归纳得到数列的通项公式,然后利用数学归纳法证明.
解答 解:(1)由a1=1,$\frac{{a}_{n+1}}{{a}_{n}+1}$=$\frac{n+2}{n}$,得${a}_{n+1}=\frac{(n+2)({a}_{n}+1)}{n}$,
则a2=6,a3=14,a4=25;
(2)由(1)可知,${a}_{1}=\frac{1×2}{2},{a}_{2}=6=\frac{4×3}{2},{a}_{3}=14=\frac{7×4}{2}$$,{a}_{4}=25=\frac{10×5}{2}$.
猜想${a}_{n}=\frac{(3n-2)(n+1)}{2}$.
下面用数学归纳法证明上式成立:
①当n=1时,$\frac{(3n-2)(n+1)}{2}=1={a}_{1}$,结论成立;
②假设当n=k(k∈N*)时,结论成立,即${a}_{k}=\frac{(3k-2)(k+1)}{2}$,
那么,当n=k+1时,${a}_{k+1}=\frac{(k+2)({a}_{k}+1)}{k}$=$\frac{(k+2)[\frac{(3k-2)(k+1)}{2}+1]}{k}$=$\frac{(k+2)(3{k}^{2}+k)}{2k}=\frac{(3k+1)(k+2)}{2}$.
故当n=k+1时,结论成立.
综上所述,对n∈N*,总有${a}_{n}=\frac{(3n-2)(n+1)}{2}$.
点评 本题考查数列递推式,考查了利用数学归纳法证明数列的通项公式,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
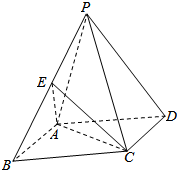 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,△PAD是正三角形,四边形ABCD是矩形,且AD=$\sqrt{2}$AB,E为PB的中点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,△PAD是正三角形,四边形ABCD是矩形,且AD=$\sqrt{2}$AB,E为PB的中点.