题目内容
20.已知x2-2ax+3a-1>0,x∈(0,+∞),求a的取值范围.分析 对x讨论,当x=$\frac{3}{2}$时,不等式显然成立;当0<x<$\frac{3}{2}$时,当x>$\frac{3}{2}$时,运用参数分离,及基本不等式,结合恒成立思想即可得到所求范围.
解答 解:x2-2ax+3a-1>0即为
(x2-1)+a(3-2x)>0,①
当x=$\frac{3}{2}$时,①显然成立;
当0<x<$\frac{3}{2}$时,①可化为a>$\frac{1-{x}^{2}}{3-2x}$,
令t=3-2x(t>0),则a>$\frac{1}{4}$(6-t-$\frac{5}{t}$),
而t+$\frac{5}{t}$≥2$\sqrt{5}$,当且仅当t=$\sqrt{5}$取得最小值.
即有$\frac{1}{4}$(6-t-$\frac{5}{t}$)≤$\frac{3-\sqrt{5}}{2}$,即有a>$\frac{3-\sqrt{5}}{2}$;
当x>$\frac{3}{2}$时,①可化为a<$\frac{1-{x}^{2}}{3-2x}$,
令t=3-2x(t<0),则a<$\frac{1}{4}$(6-t-$\frac{5}{t}$),
而-t+(-$\frac{5}{t}$)≥2$\sqrt{5}$,当且仅当t=-$\sqrt{5}$取得最小值.
即有$\frac{1}{4}$(6-t-$\frac{5}{t}$)≥$\frac{3+\sqrt{5}}{2}$,
即有a<$\frac{3+\sqrt{5}}{2}$.
综上可得$\frac{3-\sqrt{5}}{2}$<a<$\frac{3+\sqrt{5}}{2}$.
点评 本题考查函数的恒成立问题,注意运用参数分离和基本不等式求最值,考查运算能力,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
8.为了解某大学的学生是否爱好体育锻炼,用简单随机抽样方法在校园内调查了120位学生,得到如下2×2列联表:
则a-b-c等于( )
| 男 | 女 | 总计 | |
| 爱好 | a | b | 73 |
| 不爱好 | c | 25 | |
| 总计 | 74 |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
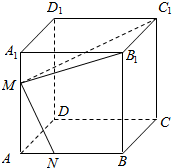 在正方体ABCD-A1B1C1D1中,M,N分别是A1A,AB上的点,若∠NMC1=90°,求证:NM⊥MB1.
在正方体ABCD-A1B1C1D1中,M,N分别是A1A,AB上的点,若∠NMC1=90°,求证:NM⊥MB1.