题目内容
【题目】如图，在三棱锥
中，
，
，
，且
，
，
，
，
为
上一点，
.
（1）求证：
平面
；
（2）求异面直线
和
所成角的余弦值.
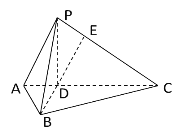
【答案】(1)见解析（2）
【解析】
（1）要证明DE∥平面PAB，只需证DE与平面PAB内的一条直线平行即可．（2）由（1）知DE∥AP．则异面直线AB和DE所成角即AB和AP所成的角，由余弦定理计算即可．
（1）证明：∵AD=1，CD=2，
∴在
中，
∴DE∥AP．
∵AP平面PAB，DE平面PAB，
∴DE∥平面PAB；
（2）解：由（1）知DE∥AP．则异面直线AB和DE所成角即AB和AP所成的角．∵PD⊥AC，AD=1，PD=2，在
中，AP2=AD2+PD2=12+22=5．
∵BD⊥AC，AD=1，BD=1，在
中，AB2=AD2+BD2=12+12=2．
∵PD⊥BD，PD=2，在
中，PB2=PD2+BD2=22+12=5．
在
中，cos∠PAB= 
,
∴异面直线
和
所成角的余弦值为.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】甲、乙两所学校高三年级分别有600人，500人，为了解两所学校全体高三年级学生在该地区五校联考的数学成绩情况，采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
甲校：
分组 | [70，80） | [80，90） | [90，100） | [100，110） |
频数 | 3 | 4 | 7 | 14 |
分组 | [110，120） | [120，130） | [130，140） | [140，150] |
频数 | 17 | x | 4 | 2 |
乙校：
分组 | [70，80） | [80，90） | [90，100） | [100，110） |
频数 | 1 | 2 | 8 | 9 |
分组 | [110，120） | [120，130） | [130，140） | [140，150] |
频数 | 10 | 10 | y | 4 |
（1）计算x，y的值；
（2）若规定考试成绩在[120，150]内为优秀，由以上统计数据填写下面的2×2列联表，并判断是否有90%的把握认为两所学校的数学成绩有差异；
（3）若规定考试成绩在[120，150]内为优秀，现从已抽取的110人中抽取两人，要求每校抽1人，所抽的两人中有人优秀的条件下，求乙校被抽到的同学不是优秀的概率．
甲校 | 乙校 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
参考公式：K2= 
，其中n=a+b+c+d．
临界值表：
P（K2≥k0） | 0.10 | 0.05 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
