题目内容
【题目】如图，在三棱锥中，SA=SB=AB=BC=CA=6，且侧面ASB⊥底面ABC，则三棱锥S－ABC外接球的表面积为（ ）
A. 60π B. 56π C. 52π D. 48π
【答案】A
【解析】
如图，设D为AB中点，O1为△ABC的外心，O2为△SAB的外心，O为三棱锥S－ABC外接球的球心，球O的半径为R.
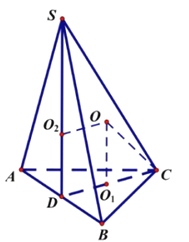
由SA=SB=AB=BC=CA=6，知△SAB、△ABC是边长为6的正三角形.
∴SD⊥AB，CD⊥AB，CD=SD=
，O1在CD上，O2在SD上，且O2D= O1D=
，CO1=
.
∵侧面ASB⊥底面ABC，OO1⊥面ABC，
∴SD⊥面ABC，O2D⊥O1D，SD∥OO1.
∴四边形O2DO1O为正方形，OO1=O2D=.
∴
.
∴三棱锥S－ABC外接球的表面积为4πR2=60π.选A.
练习册系列答案
53随堂测系列答案
相关题目
