题目内容
设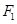 、
、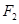 分别为双曲线
分别为双曲线 的左、右焦点.若在双曲线右支上存在点
的左、右焦点.若在双曲线右支上存在点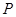 ,满足
,满足 ,且
,且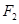 到直线
到直线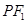 的距离等于双曲线的实轴长,则该双曲线的离心率为( )
的距离等于双曲线的实轴长,则该双曲线的离心率为( )
A. | B. | C.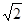 | D.2 |
B
解析试题分析:如图, 为
为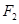 到直线
到直线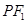 的距离,则
的距离,则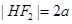 ,因为
,因为
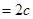 ,所以
,所以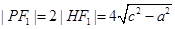 ,又因为
,又因为 ,所以
,所以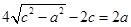 ,解得
,解得 。故选B。
。故选B。
考点:双曲线的性质
点评:解关于曲线的问题,要想到这种曲线有什么特点。像本题,要利用双曲线上的点到两焦点的距离之差的绝对值等于2a这样的特点来解答。

练习册系列答案
相关题目
若双曲线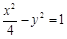 的渐近线与圆
的渐近线与圆 (
(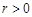 )相切,则
)相切,则
| A.5 | B.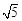 | C.2 | D. |
若双曲线 的离心率是2,则实数k的值是 ( )
的离心率是2,则实数k的值是 ( )
| A.—3 | B.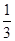 | C.3 | D.—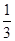 |
双曲线 的渐近线方程为( )
的渐近线方程为( )
A. | B. | C. | D. |
设 、
、 是双曲线
是双曲线 的左、右两个焦点,若双曲线右支上存在一点P,使
的左、右两个焦点,若双曲线右支上存在一点P,使 ,且
,且 ,则
,则 的值为( )
的值为( )
| A.2 | B. | C.3 | D. |
 ,则双曲线的的离心率为( )
,则双曲线的的离心率为( )

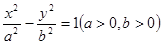 的左右焦点分别是
的左右焦点分别是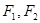 ,设
,设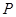 是双曲线右支上一点,
是双曲线右支上一点,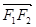 在
在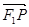 上投影的大小恰好为
上投影的大小恰好为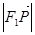 ,且它们的夹角为
,且它们的夹角为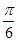 ,则双曲线的离心率为( )
,则双曲线的离心率为( )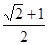
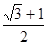
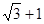
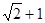
 (
(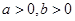 )的右焦点
)的右焦点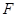 作圆
作圆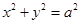 的切线
的切线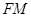 ,交
,交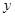 轴于点
轴于点 ,切圆于点
,切圆于点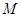 ,若
,若 ,则双曲线的离心率是( )
,则双曲线的离心率是( )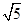


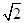
 为C的实轴长的2倍,则双曲线C的离心率为( )
为C的实轴长的2倍,则双曲线C的离心率为( )