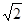题目内容
双曲线 的渐近线方程为( )
的渐近线方程为( )
A. | B. | C. | D. |
C
解析试题分析:因为双曲线 可以表示为
可以表示为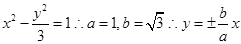 为其渐近线方程,因此可知为
为其渐近线方程,因此可知为 ,故选C.
,故选C.
考点:双曲线的性质
点评:主要是考查了双曲线的渐近线方程的求解,属于基础题。

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
抛物线 上的一动点
上的一动点 到直线
到直线 距离的最小值是 ( )
距离的最小值是 ( )
A. | B. | C. | D. |
抛物线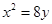 的焦点坐标是 ( )
的焦点坐标是 ( )
| A.(0,2) | B.(0,-2) | C.(4,0) | D.(-4,0) |
极坐标方程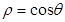 和参数方程
和参数方程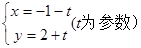 所表示的图形分别是( )
所表示的图形分别是( )
| A.直线,直线 | B.直线,圆 |
| C.圆,圆 | D.圆,直线 |
已知双曲线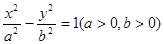 的渐近线与圆
的渐近线与圆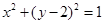 相切,则双曲线的离心率为( )
相切,则双曲线的离心率为( )
A.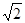 | B.2 | C.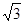 | D.3 |
设F为抛物线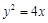 的焦点,
的焦点,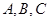 为抛物线上不同的三点,点
为抛物线上不同的三点,点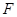 是△ABC的重心,
是△ABC的重心, 为坐标原点,△
为坐标原点,△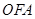 、△
、△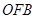 、△
、△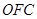 的面积分别为
的面积分别为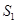 、
、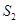 、
、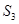 ,则
,则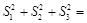 ( )
( )
| A.9 | B.6 | C.3 | D.2 |
顶点在原点,经过圆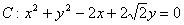 的圆心且准线与
的圆心且准线与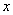 轴垂直的抛物线方程为
轴垂直的抛物线方程为
A.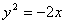 | B.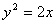 |
C.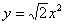 | D.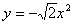 |
已知双曲线 :
:
 的离心率
的离心率 ,过双曲线
,过双曲线 的左焦点
的左焦点 作
作 :
: 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,则
,则 的大小等于( )
的大小等于( )
| A.45° | B.60° | C.90° | D.120° |
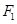 、
、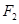 分别为双曲线
分别为双曲线 的左、右焦点.若在双曲线右支上存在点
的左、右焦点.若在双曲线右支上存在点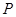 ,满足
,满足 ,且
,且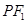 的距离等于双曲线的实轴长,则该双曲线的离心率为( )
的距离等于双曲线的实轴长,则该双曲线的离心率为( )