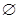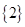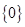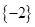题目内容
已知集合M={x|x2-x=0},N={x|a(2x+1)<1,若M⊆N,则实数a的取值范围是______.
集合M={x|x2-x=0}={0,1},
①当a>0时,则a(2x+1)<1?2x+1<
?x<
-
由于M⊆N,则
-
>1,解得a<
故实数a的取值范围:0<a<
;
②当a=0时,则a(2x+1)<1?0<1恒成立
显然满足M⊆N,故a=0;
③当a<0时,则a(2x+1)<1?2x+1>
?x>
-
由于M⊆N,则
-
<0,解得a<0
故实数a的取值范围:a<0;
综上可知,实数a的取值范围:a<
.
故答案为 a<
①当a>0时,则a(2x+1)<1?2x+1<
| 1 |
| a |
| 1 |
| 2a |
| 1 |
| 2 |
由于M⊆N,则
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 3 |
故实数a的取值范围:0<a<
| 1 |
| 3 |
②当a=0时,则a(2x+1)<1?0<1恒成立
显然满足M⊆N,故a=0;
③当a<0时,则a(2x+1)<1?2x+1>
| 1 |
| a |
| 1 |
| 2a |
| 1 |
| 2 |
由于M⊆N,则
| 1 |
| 2a |
| 1 |
| 2 |
故实数a的取值范围:a<0;
综上可知,实数a的取值范围:a<
| 1 |
| 3 |
故答案为 a<
| 1 |
| 3 |

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
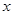 |
|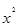 -
-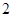
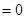 ﹜,则A
﹜,则A B=
B=