题目内容
设A={1,3,a},B={1,a2-a+1},若B⊆A,则a的值为( )
| A.2或1 | B.2或-1 | C.-2或1 | D.1或-1 |
∵A={1,3,a},B={1,a2-a+1},
若B⊆A,则a2-a+1=3或a2-a+1=a,
即a2-a-2=0或a2-2a+1=0,
解得a=1或a=-1或a=2.
当a=1时,A={1,1,3}不成立.
∴a=-1或a=2.
故选:B.
若B⊆A,则a2-a+1=3或a2-a+1=a,
即a2-a-2=0或a2-2a+1=0,
解得a=1或a=-1或a=2.
当a=1时,A={1,1,3}不成立.
∴a=-1或a=2.
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
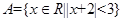 ,集合
,集合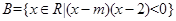 且
且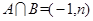 ,则
,则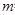 +
+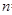 = .
= .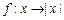 是集合A到集合B的映射,且集合B中的每一个元素都有原象,若
是集合A到集合B的映射,且集合B中的每一个元素都有原象,若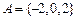 ,则
,则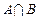 等于()
等于()