题目内容
已知F1,F2分别是椭圆E: +y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.
+y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.
(1)求圆C的方程;
(2)设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a,b.当ab最大时,求直线l的方程.
 +y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.
+y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.(1)求圆C的方程;
(2)设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a,b.当ab最大时,求直线l的方程.
(1)(x-2)2+(y-2)2=4 (2)x-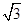 y-2=0或x+
y-2=0或x+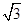 y-2=0
y-2=0
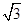 y-2=0或x+
y-2=0或x+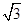 y-2=0
y-2=0解:(1)由题设知,F1,F2的坐标分别为(-2,0),(2,0),圆C的半径为2,圆心为原点O关于直线x+y-2=0的对称点.
设圆心的坐标为(x0,y0),
由
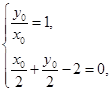 解得
解得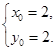
所以圆C的方程为(x-2)2+(y-2)2=4.
(2)由题意,可设直线l的方程为x=my+2,
则圆心到直线l的距离d=
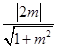 .
.所以b=2
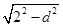 =
=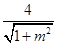 .
.由
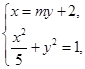 得(m2+5)y2+4my-1=0.
得(m2+5)y2+4my-1=0.设l与E的两个交点坐标分别为(x1,y1),(x2,y2),
则y1+y2=-
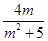 ,y1y2=-
,y1y2=-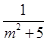 .
.于是a=
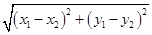 =
=
=
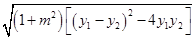
=
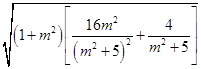 =
= .
.从而ab=
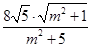 =
=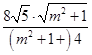
=
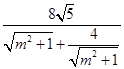 ≤
≤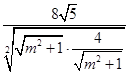
=2
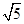 .
.当且仅当
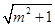 =
=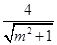 ,即m=±
,即m=±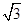 时等号成立.
时等号成立.故当m=±
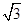 时,ab最大,此时,直线l的方程为x=
时,ab最大,此时,直线l的方程为x=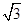 y+2或x=-
y+2或x=-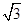 y+2,
y+2,即x-
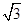 y-2=0或x+
y-2=0或x+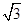 y-2=0.
y-2=0.
练习册系列答案
相关题目

 :
: ,圆
,圆 :
:
 ,过圆
,过圆 作圆
作圆 、
、 ,切点分别为
,切点分别为 、
、 ,则
,则 的最小值是( )
的最小值是( )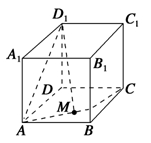
 :
: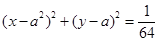
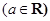 ,则下列命题:①圆
,则下列命题:①圆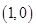 的最短距离的最小值为
的最短距离的最小值为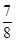 ;②圆
;②圆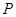 到点
到点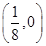 的距离与到直线
的距离与到直线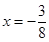 的距离相等;③已知
的距离相等;③已知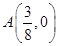 ,在圆
,在圆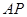 为直径的圆与直线
为直径的圆与直线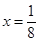 相切.真命题的个数为
相切.真命题的个数为

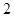

 在圆
在圆 的内部,则
的内部,则 的取值范围是( )
的取值范围是( )