题目内容
设圆C同时满足三个条件:①过原点;②圆心在直线y=x
上;③截y轴所得的弦长为4,则圆C的方程是 .
上;③截y轴所得的弦长为4,则圆C的方程是 .
(x+2)2+(y+2)2=8或(x-2)2+(y-2)2=8
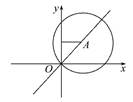
由题意可设圆心A(a,a),如图,则22+a2=2a2,解得a=±2,r2=2a2=8.所以圆C的方程是(x+2)2+(y+2)2=8或(x-2)2+(y-2)2=8.
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
芝麻开花课程新体验系列答案
，
)的直线
与圆
相切，求直线
)且倾斜角为
的直线
两点，求线段
的中点
的坐标；
的直线
,且以
（-1,1），
（1,3）.
两点的直线方程；
轴上的圆的方程.
为何值时，曲线C表示圆；
交于M、N两点，且
，求
与圆
交于
，
两点，是否存在实数
为直径的圆过原点，若存在，求出实数
+y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.