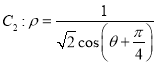题目内容
【题目】已知极点为直角坐标系的原点，极轴为x轴正半轴且单位长度相同的极坐标系中曲线
，
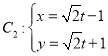（t为参数）.
（1）求曲线
上的点到曲线
距离的最小值；
（2）若把上各点的横坐标都扩大到原来的2倍，纵坐标都扩大到原来的
倍，得到曲线
，设
，曲线与交于A，B两点，求
.
【答案】（1）
；（2）
【解析】
（1）根据题意，将
的极坐标方程转化成直角坐标方程，将
的参数方程化成普通方程，利用几何法，计算曲线上的点到曲线距离的最小值.
（2）根据伸缩变换，写出曲线
的直角坐标方程，再根据直线的参数方程化成标准方程，利用参数t的几何意义，计算即可求解.
（1）
，圆心为
，半径为1，
圆心到直线距离
，
所以上的点到的最小距离为；
（2）伸缩变换为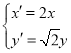
，所以
，
把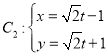
（t为参数）化成标准方程为：
，
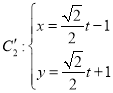将
和
联立，得
，
因为
，
∴
.
练习册系列答案
相关题目
