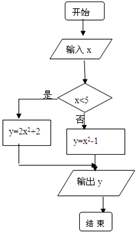
用分析法证明:已知a＞b＞0.求证$\sqrt{a}$-$\sqrt{b}$＜$\sqrt{a-b}$．题目和参考答案——青夏教育精英家教网—

题目内容

17．用分析法证明：已知a＞b＞0，求证$\sqrt{a}$-$\sqrt{b}$＜$\sqrt{a-b}$．

分析根据题意，将原不等式两边平方，整理，利用分析法即可得证．

解答证明：∵a＞b＞0，∴$\sqrt{a}$＞$\sqrt{b}$，
∴要证$\sqrt{a}$-$\sqrt{b}$＜$\sqrt{a-b}$，只需证（$\sqrt{a}-\sqrt{b}$）²$＜（\sqrt{a-b}）^{2}$，
即a+b-2$\sqrt{ab}$＜a-b，只需证b$＜\sqrt{ab}$，即证b＜a，
显然b＜a成立，
因此$\sqrt{a}$-$\sqrt{b}$＜$\sqrt{a-b}$成立．

点评本题主要考查了用分析法证明不等式，属于基本知识的考查．

练习册系列答案

相关题目

7．如图是一个算法的流程图，回答下面的问题：当输入的值为3时，输出的结果为20

8．极坐标方程（ρ-1）（θ-π）=0（ρ≥0）表示的图形是一个圆和一条射线．

5．曲线f（x）=x+2^xlnx在点（1，1）处的切线的斜率等于（　　）

12．已知函数f（x）=ax³+bx²，在x=1时有极大值3；
（Ⅰ）求a，b的值；
（Ⅱ）求函数f（x）在[-1，2]上的最值．

2．已知函数$f（x）=x+\frac{a^2}{x}$，g（x）=x+lnx，其中a＞0．
（1）若x=1是函数h（x）=f（x）+g（x）的极值点，求实数a的值；
（2）若对任意的x₁，x₂∈[1，e]（e为自然对数的底数）都有f（x₁）≥g（x₂）成立，求实数a的取值范围．

9．已知函数$f（x）=2sin（ωx+\frac{π}{3}）$，且ω≠0，ω∈R．
（Ⅰ）若函数f（x）的图象经过点$（\frac{π}{3}\;，2）$，且0＜ω＜3，求ω的值；
（Ⅱ）在（Ⅰ）的条件下，若函数g（x）=mf（x）+n（m＞0），当$x∈[-2π，-\frac{π}{3}]$时，函数g（x）的值域为[-2，1]，求m，n的值；
（Ⅲ）若函数$h（x）=f（x-\frac{π}{3ω}）$在$[-\frac{π}{3}\;，\frac{π}{3}]$上是减函数，求ω的取值范围．

6．已知数列{a_n}满足a₁=$\frac{1}{2}$，a_n=4a_n-1+1（n≥2）．
（1）令b_n=a_n+$\frac{1}{3}$，求证数列{b_n}是等比数列；
（2）求数列{b_n}的前n项和T_n．

7．通过随机询问110名性别不同的大学生是否爱好某项运动，计算Χ²≈7.6参照参考数据，得到的正确结论是（　　）

	A．	有99%以上的把握认为“爱好该项运动与性别有关”
	B．	有99%以上的把握认为“爱好该项运动与性别无关”
	C．	有90%以上的把握认为“爱好该项运动与性别有关”
	D．	有90%以上的把握认为“爱好该项运动与性别无关”

试题分类