[题目]支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题::恰有四支球队并列第一名为不可能事件, :有可能出现恰有两支球队并列第一名,:每支球队都既有胜又有败的概率为, :五支球队成绩并列第一题目和参考答案——青夏教育精英家教网—

题目内容

【题目】支篮球队进行单循环比赛（任两支球队恰进行一场比赛）,任两支球队之间胜率都是.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题：

：恰有四支球队并列第一名为不可能事件；：有可能出现恰有两支球队并列第一名；

：每支球队都既有胜又有败的概率为；：五支球队成绩并列第一名的概率为.

其中真命题是

A. ,, B. ,, C. .. D. ..

【答案】A

【解析】支球队单循环，共举行场比赛，共有次胜次负．由于以获胜场次数作为球队的成绩．就算四支球队都胜场，则第五支球队也无法胜场，若四支球队都胜场，则第五支球队也胜场，五支球队并列第一，除此不会再有四支球队胜场次数相同．故是真命题；会出现两支球队胜场，剩下三支球队中两支球队各胜场，另一支球队胜场的情况，此时两支球队并列第一名．故为真命题；由题可知球队成绩并列第一名，各胜一场的概率为小于．排除．故本题答案选．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

【题目】随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查人,并将调查情况进行整理后制成下表：

年龄（岁）
频数
赞成人数

（1）世界联合国卫生组织规定: 岁为青年，为中年，根据以上统计数据填写以下列联表：

	青年人	中年人	合计
不赞成
赞成
合计

（2）判断能否在犯错误的概率不超过的前提下，认为赞成“车柄限行”与年龄有关？

附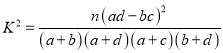：，其中

独立检验临界值表：

（3）若从年龄的被调查中各随机选取人进行调查，设选中的两人中持不赞成“车辆限行”态度的人员为，求随机变量的分布列和数学期望.

【题目】函数f（x）=Asin（ωx+）（A，ω，是常数，A＞0，ω＞0）的部分图象如图所示，下列结论： ①最小正周期为π；
②将f（x）的图象向左平移个单位，所得到的函数是偶函数；
③f（0）=1；
④ ；
⑤ ．
其中正确的是（）

A.①②③
B.②③④
C.①④⑤
D.②③⑤

【题目】已知关于x的二次函数f（x）=ax2﹣4bx+1
（Ⅰ）设集合P={1，2，3}，集合Q={﹣1，1，2，3，4}，从集合P中随机取一个数作为a，从集合Q中随机取一个数作为b，求函数f（x）在区间[1，+∞）上是增函数的概率；
（Ⅱ）设点（a，b）是区域内的随机点，求函数f（x）在区间[1，+∞）上是增函数的概率．

【题目】已知椭圆C方程为（a＞b＞0），左、右焦点分别是F1 ， F2 ，若椭圆C上的点P（1，）到F1 ， F2的距离和等于4．（Ⅰ）写出椭圆C的方程和焦点坐标；
（Ⅱ）设点Q是椭圆C的动点，求线段F1Q中点T的轨迹方程；
（Ⅲ）直线l过定点M（0，2），且与椭圆C交于不同的两点A，B，若∠AOB为锐角（O为坐标原点），求直线l的斜率k0的取值范围．

【题目】在平面直角坐标系xOy中，圆C的方程为x2+y2﹣8x+15=0，若直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是．

【题目】已知方程x2+y2﹣2x﹣4y+m=0．
（1）若此方程表示圆，求m的取值范围；
（2）若（1）中的圆与直线x+2y﹣4=0相交于M、N两点，且OM⊥ON（O为坐标原点），求m；
（3）在（2）的条件下，求以MN为直径的圆的方程．

【题目】定义在（﹣∞，0）∪（0，+∞）上的函数f（x），如果对于任意给定的等比数列{an}，{f（an）}仍是等比数列，则称f（x）为“保等比数列函数”．现有定义在（﹣∞，0）∪（0，+∞）上的如下函数：①f（x）=x2；②f（x）=2x；③f（x）= ；④f（x）=ln|x|．则其中是“保等比数列函数”的f（x）的序号为（）
A.①②
B.③④
C.①③
D.②④

【题目】已知函数f（x）=loga（x+2）+loga（3﹣x），其中0＜a＜1．
（1）求函数f（x）的定义域；
（2）若函数f（x）的最小值为﹣4，求a的值．

试题分类