Question

【题目】已知椭圆C方程为 （a＞b＞0），左、右焦点分别是F1 ， F2 ， 若椭圆C上的点P（1， ）到F1 ， F2的距离和等于4． （Ⅰ）写出椭圆C的方程和焦点坐标；
（Ⅱ）设点Q是椭圆C的动点，求线段F1Q中点T的轨迹方程；
（Ⅲ）直线l过定点M（0，2），且与椭圆C交于不同的两点A，B，若∠AOB为锐角（O为坐标原点），求直线l的斜率k0的取值范围．

Answer 1

【答案】解：（Ⅰ）由题意得：2a=4，得a=2， 又点P（1， ）在椭圆 上，
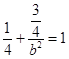∴ ，解得b2=1．
∴椭圆C的方程为 ，焦点 ；
（Ⅱ）设椭圆上的动点Q（x0 ， y0），线段F1Q中点T（x，y），
由题意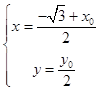得： ，得 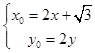，代入椭圆的方程得 ，
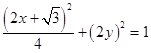即 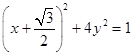为线段F1Q中点T的轨迹方程；
（Ⅲ）由题意得直线l的斜率存在且不为0，
设l：y=kx+2，代入 整理，
得（1+4k2）x2+16kx+12=0，
△=（16k）2﹣4（1+4k2）12=16（4k2﹣3）＞0，得 　 …①
设A（x1 ， y1），B（x2 ， y2），∴ ．
∵∠AOB为锐角，
∴cos∠AOB＞0，则 ，
又 ．
∴
=
= ，
∴k2＜4 …②
由①、②得 ．
∴k的取值范围是 ．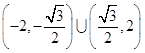
【解析】（Ⅰ）由题意得到椭圆的半长轴长，把点P的坐标代入椭圆方程求得b，则椭圆方程可求；（Ⅱ）设出Q和T的坐标，由中点坐标公式把Q的坐标用T的坐标表示，代入椭圆方程可得线段F1Q中点T的轨迹方程；（Ⅲ）联立直线和椭圆方程，化为关于x的应用二次方程，由判别式大于0及 求解直线l的斜率的取值范围．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．