题目内容
【题目】已知关于x的二次函数f(x)=ax2﹣4bx+1
(Ⅰ)设集合P={1,2,3},集合Q={﹣1,1,2,3,4},从集合P中随机取一个数作为a,从集合Q中随机取一个数作为b,求函数f(x)在区间[1,+∞)上是增函数的概率;
(Ⅱ)设点(a,b)是区域 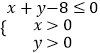 内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
【答案】解(Ⅰ)∵函数f(x)=ax2﹣4bx+1的图象的对称轴为x= ![]() ,
,
要使f(x)=ax2﹣4bx+1在区间[1,+∞)上为增函数,
当且仅当a>0且x= ![]() ≤1,
≤1,
即2b≤a.
若a=1,则b=﹣1;
若a=2,则b=﹣1,1;
若a=3,则b=﹣1,1,
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为 ![]() .
.
(Ⅱ)由(1)知当且仅当2b≤a.且a>0时,
函数f(x)=ax2﹣4bx+1在区间[1,+∞)上为增函数,
依条件可知试验的全部结果所构成的区域为{ 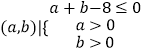 }
}
构成所求事件的区域为三角形部分.
由 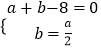 ,解得a=
,解得a= ![]() ,b=
,b= ![]() ,即交点坐标(
,即交点坐标( ![]() ,
, ![]() ),
),
∴所求事件的概率为P= 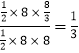
【解析】(Ⅰ)根据古典概率的概率公式进行计算即可求出概率.(Ⅱ)根据几何概型的概率公式进行计算即可.
【考点精析】根据题目的已知条件,利用二元一次不等式(组)所表示的平面区域和几何概型的相关知识可以得到问题的答案,需要掌握不等式组表示的平面区域是各个不等式所表示的平面区域的公共部;几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.

练习册系列答案
相关题目