题目内容
【题目】已知抛物线![]() 的焦点F,C上一点
的焦点F,C上一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求C的方程;
(2)过F作直线l,交C于A,B两点,若直线AB中点的纵坐标为![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)![]() .
.
(2)![]() .
.
【解析】
![]() 法一:利用已知条件列出方程组,求解即可
法一:利用已知条件列出方程组,求解即可
法二:利用抛物线![]() 的准线方程,由抛物线的定义列出方程,求解即可
的准线方程,由抛物线的定义列出方程,求解即可
![]() 法一:由
法一:由![]() 可得抛物线焦点
可得抛物线焦点![]() 的坐标,设出
的坐标,设出![]() 两点的坐标,利用点差法,求出线段
两点的坐标,利用点差法,求出线段![]() 中点的纵坐标为
中点的纵坐标为![]() ,得到直线的斜率,求出直线方程
,得到直线的斜率,求出直线方程
法二:设直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程,设出
,联立直线与抛物线方程,设出![]() 两点的坐标,通过线段
两点的坐标,通过线段![]() 中点的纵坐标为
中点的纵坐标为![]() ,求出
,求出![]() 即可
即可
法一:抛物线![]() :
: ![]() 的焦点
的焦点![]() 的坐标为
的坐标为![]() ,由已知
,由已知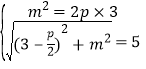
解得![]() 或
或![]() ∵
∵![]() ,
,
∴![]() ∴
∴![]() 的方程为
的方程为![]() .
.
法二:抛物线![]() 的准线方程为
的准线方程为![]() 由抛物线的定义可知
由抛物线的定义可知![]() 解得
解得![]()
∴![]() 的方程为
的方程为![]() .
.
2.法一:由(1)得抛物线C的方程为![]() ,焦点
,焦点![]()
设![]() 两点的坐标分别为
两点的坐标分别为![]() ,则
,则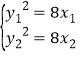
两式相减,整理得![]()
∵线段![]() 中点的纵坐标为
中点的纵坐标为![]()
∴直线![]() 的斜率
的斜率![]()
直线![]() 的方程为
的方程为![]() 即
即![]()
分法二:由(1)得抛物线![]() 的方程为
的方程为![]() ,焦点
,焦点![]()
设直线![]() 的方程为
的方程为![]() 由
由![]()
消去![]() ,得
,得![]() 设
设![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,
∵线段![]() 中点的纵坐标为
中点的纵坐标为![]() ∴
∴![]() 解得
解得![]()
直线![]() 的方程为
的方程为![]() 即
即![]()

【题目】学校高三数学备课组为了更好地制定复习计划,开展了试卷讲评后效果的调研,从上学期期末数学试题中选出一些学生易错题,重新进行测试,并认为做这些题不出任何错误的同学为“过关”,出了错误的同学为“不过关”,现随机抽查了年级50人,他们的测试成绩的频数分布如下表:
期末分数段 |
|
|
|
|
|
|
人数 | 5 | 10 | 15 | 10 | 5 | 5 |
“过关”人数 | 1 | 2 | 9 | 7 | 3 | 4 |
(1)由以上统计数据完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为期末数学成绩不低于90分与测试“过关”有关?说明你的理由:
的把握认为期末数学成绩不低于90分与测试“过关”有关?说明你的理由:
分数低于90分人数 | 分数不低于90分人数 | 合计 | |
“过关”人数 | |||
“不过关”人数 | |||
合计 |
(2)在期末分数段![]() 的5人中,从中随机选3人,记抽取到过关测试“过关”的人数为
的5人中,从中随机选3人,记抽取到过关测试“过关”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |