题目内容
任意的实数k,直线 与圆
与圆 的位置关系一定是 ( )
的位置关系一定是 ( )
| A.相离 | B.相切 | C.相交但直线不过圆心 | D.相交且直线过圆心 |
D
解析试题分析:方法一 利用圆心到直线的距离与半径的大小比较求解 圆
圆 的圆心
的圆心 到直线
到直线 的距离为
的距离为 ‘
‘
又
 ,
,
 ,
, 直线与圆相交但直线不过圆心。
直线与圆相交但直线不过圆心。
方法二 利用直线方程与圆的方程联立的方程组的根的个求解
联立 得
得 (*)
(*)

故(*)有两个不等的实数根,所以方程组有两组解,又直线显然过原点
所以直线与圆相交但不过圆心.
考点:本小题主要考查了直线与圆的位置关系的判定(几何法、代数法)及点到直线的距离公式,方程组的解的判定,同时考查了运算求解能力。
点评:解决此类问题的关键是掌握直线与圆的位置关系的判定方法,并能熟练应用。直线与圆的位置关系的判定多用几何法,难度较小。

练习册系列答案
相关题目
当点P在圆x2+y2=1上变动时,它与定点Q (3,0) 相连,线段PQ的中点M的轨迹方程是( )
| A.(x+3)2+y2=4 | B.(x-3)2+y2=1 |
| C.(2x-3)2+4y2=1 | D.(2x+3)2+4y2=1 |
设 ,若线段
,若线段 是△
是△ 外接圆的直径,则点
外接圆的直径,则点 的坐标是( ).
的坐标是( ).
| A.(-8,6) | B.(8,-6) | C.(4,-6) | D.(4,-3) |
点 与圆
与圆 上任一点连线的中点轨迹方程是( )
上任一点连线的中点轨迹方程是( )
A. | B. |
C. | D. |
圆 :
: 与圆
与圆 公切线的条数是( )
公切线的条数是( )
| A.0条 | B.1条 | C.2条 | D.3条 |
直线 与圆
与圆 相切,则
相切,则 的值为 ( )
的值为 ( )
A. | B. | C.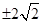 | D. |
已知直线 与圆
与圆 交于
交于 两点,且
两点,且 ,则实数
,则实数 的值为( )
的值为( )
| A.2 | B.-2 | C.2或-2 | D. 或 或 |
 的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).
的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).
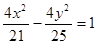



 表示圆,则
表示圆,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.