题目内容
圆 :
: 与圆
与圆 公切线的条数是( )
公切线的条数是( )
| A.0条 | B.1条 | C.2条 | D.3条 |
C
解析试题分析: 的圆心为
的圆心为 ;
; 的圆心为
的圆心为 ,所以
,所以 ,所以两圆相交,所以两圆公切线的条数为2条.
,所以两圆相交,所以两圆公切线的条数为2条.
考点:本小题主要考查圆与圆的位置关系的判断.
点评:判断圆与圆的位置关系主要是判断圆心距与半径的和与差之间的关系,而不要联立方程组,那样运算量太大.

练习册系列答案
相关题目
方程x2+y2+2x-4y-6=0表示的图形是( )
A.以(1,-2)为圆心, 为半径的圆; 为半径的圆; | B.以(1,2)为圆心, 为半径的圆; 为半径的圆; |
C.以(-1,-2)为圆心, 为半径的圆; 为半径的圆; | D.以(-1,2)为圆心, 为半径的圆 为半径的圆 |
已知直线l:3x+4y-12=0与圆C: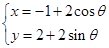 (θ为参数)的位置关系是( )
(θ为参数)的位置关系是( )
| A.相切 | B.相离 | C.相交但直线不过圆心 | D.直线过圆心 |
任意的实数k,直线 与圆
与圆 的位置关系一定是 ( )
的位置关系一定是 ( )
| A.相离 | B.相切 | C.相交但直线不过圆心 | D.相交且直线过圆心 |
若圆 关于直线
关于直线
 对称,则直线的斜率是( )
对称,则直线的斜率是( )
| A.6 | B. | C. | D.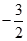 |
圆 的左、右顶点分别是
的左、右顶点分别是 ,左、右焦点分别是
,左、右焦点分别是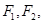 若
若 成等比数列,则此椭圆的离心率为 ( )
成等比数列,则此椭圆的离心率为 ( )
A. | B. | C. | D. |
圆心在曲线 上,且与直线2x+y+l=O相切的面积最小的圆的方程为( )
上,且与直线2x+y+l=O相切的面积最小的圆的方程为( )
A. | B.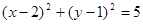 |
C. | D. |
 :
: 与圆
与圆 :
: 位置关系是( )
位置关系是( )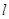 把圆
把圆 的面积平分
的面积平分 则它被这个圆截得的弦长为( )
则它被这个圆截得的弦长为( )






