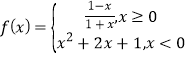题目内容
【题目】已知非单调数列{an}是公比为q的等比数列,a1=![]() ,其前n项和为Sn(n∈N*),且满足S3+a3,S5+a5,S4+a4成等差数列.
,其前n项和为Sn(n∈N*),且满足S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式和前n项和Sn;
(2)bn=![]() +
+![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】(1)![]() ,
,![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知S3+a3,S5+a5,S4+a4成等差数列构造方程解出公比q,代入等比数列的通项公式和前n项和公式可求出an与Sn;(2)由(1)求出bn=(-1)nn2+![]() ,前半部分利用分类法和等差数列求和公式求和,后半部分利用错位相减法和等比数列前n项和公式求和.
,前半部分利用分类法和等差数列求和公式求和,后半部分利用错位相减法和等比数列前n项和公式求和.
(1)∵S3+a3,S5+a5,S4+a4成等差数列,
∴2(S5+a5)=(S3+a3)+(S4+a4)
∴a3=4a5,q2=![]() ,q=-
,q=-![]() ,
,
an=![]() ·
·![]() n-1,
n-1,
∴Sn=1-![]() n.
n.
(2)bn=(-1)nn2Sn+![]() =(-1)nn2
=(-1)nn2![]() +
+![]() =(-1)nn2+
=(-1)nn2+![]() .
.
设(-1)nn2的前n项和为Hn,![]() 的前n项和为Qn
的前n项和为Qn
①当n为偶数时,
Hn=-12+22-32+42+…-(n-1)2+n2=1+2+3+4+…+n-1+n=![]() ,
,
Qn=1×![]() +2×
+2×![]() 2+…+n×
2+…+n×![]() n ①
n ①
![]() Qn=1×
Qn=1×![]() 2+…+(n-1)×
2+…+(n-1)×![]() n+n×
n+n×![]() n+1 ②
n+1 ②
①-②得,![]() Qn=
Qn=![]() +
+![]() 2+…+
2+…+![]() n-n×
n-n×![]() n+1=1-
n+1=1-![]() ,
,
∴Qn=2-![]()
∴Tn=Hn+Qn=![]() +2-
+2-![]() =
=![]() -
-![]()
②当n为奇数时,
Hn=![]() -n2=-
-n2=-![]() ,
,
∴Qn=2-![]()
∴Tn=Hn+Qn=-![]() +2-
+2-![]() =-
=-![]() -
-![]()
综合①②,∴Tn=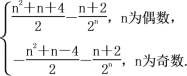

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目