题目内容
设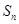 为数列
为数列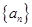 的前
的前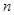 项和,且有
项和,且有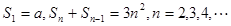
(Ⅰ)求数列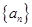 的通项公式;
的通项公式;
(Ⅱ)若数列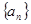 是单调递增数列,求
是单调递增数列,求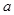 的取值范围.
的取值范围.
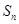 为数列
为数列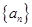 的前
的前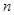 项和,且有
项和,且有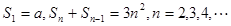
(Ⅰ)求数列
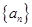 的通项公式;
的通项公式;(Ⅱ)若数列
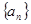 是单调递增数列,求
是单调递增数列,求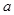 的取值范围.
的取值范围.(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
 ;(Ⅱ)
;(Ⅱ) .
.试题分析:(Ⅰ)先利用
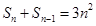 得到数列
得到数列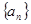 的递推公式,然后由递推公式得出数列
的递推公式,然后由递推公式得出数列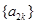 和
和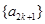 分别是以
分别是以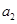 ,
,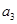 为首项,6为公差的等差数列,再用等差数列的通项公式得到分别为奇数和偶数时的递推公式,再合并即为所求;(Ⅱ)数列
为首项,6为公差的等差数列,再用等差数列的通项公式得到分别为奇数和偶数时的递推公式,再合并即为所求;(Ⅱ)数列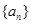 是单调递增数列
是单调递增数列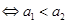 且
且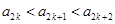 对任意的
对任意的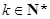 成立.然后将第(Ⅰ)问得到的通项公式代入,通过解不等式即可得到
成立.然后将第(Ⅰ)问得到的通项公式代入,通过解不等式即可得到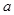 的取值范围是
的取值范围是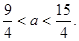
试题解析:(Ⅰ)当
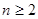 时,由已知
时,由已知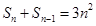 ①
①于是
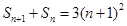 ②
②由②-①得
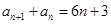 ③
③于是
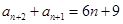 ④
④由④-③得
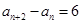 ⑤
⑤上式表明:数列
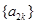 和
和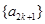 分别是以
分别是以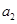 ,
,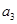 为首项,6为公差的等差数列. 4分
为首项,6为公差的等差数列. 4分又由①有
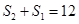 ,所以
,所以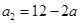 ,
,由③有
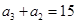 ,
,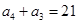 ,所以
,所以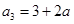 ,
,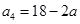 .
.所以
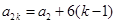
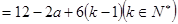 ,
,即
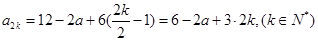 .
.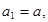
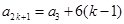
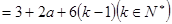 .
.即
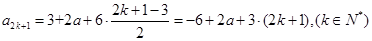 .
.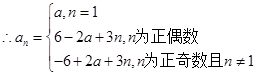 . 8分
. 8分(Ⅱ)数列
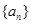 是单调递增数列
是单调递增数列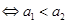 且
且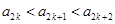 对任意的
对任意的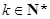 成立.
成立.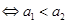 且
且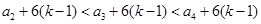
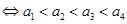
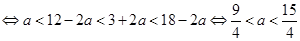 .
.所以
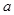 的取值范围是
的取值范围是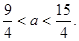 13分
13分
练习册系列答案
相关题目
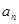 }中,
}中,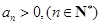 ,公比
,公比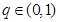 ,且
,且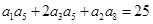 ,
, 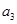 与
与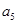 的等比中项为2.
的等比中项为2.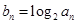 ,求:数列{
,求:数列{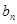 }的前
}的前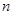 项和为
项和为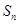 ,
,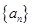 中,
中,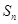 为其前n项和,若
为其前n项和,若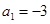 ,
,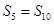 ,则当
,则当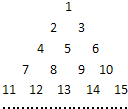
 中,
中, ,
, ,则
,则 =________.
=________. 中,
中, ,
, 则
则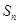 的最大值为____________.
的最大值为____________. 中,首项a1=0,公差d≠0,若
中,首项a1=0,公差d≠0,若 ,则k=( )
,则k=( )