题目内容
在等比数列{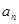 }中,
}中,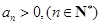 ,公比
,公比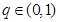 ,且
,且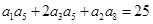 ,
, 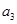 与
与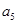 的等比中项为2.
的等比中项为2.
(1)求数列{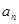 }的通项公式;
}的通项公式;
(2)设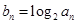 ,求:数列{
,求:数列{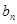 }的前
}的前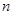 项和为
项和为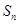 ,
,
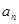 }中,
}中,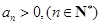 ,公比
,公比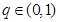 ,且
,且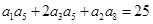 ,
, 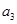 与
与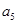 的等比中项为2.
的等比中项为2.(1)求数列{
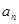 }的通项公式;
}的通项公式;(2)设
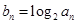 ,求:数列{
,求:数列{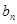 }的前
}的前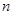 项和为
项和为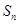 ,
,(1)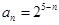 (2)
(2)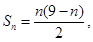
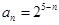 (2)
(2)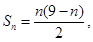
试题分析:(1)由a1a5=
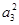 ,a2a8=
,a2a8=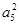 原式可化为
原式可化为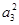 +2a3a5+
+2a3a5+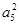 =25,即a3+a5=5,又由a3a5=4,解出q,a1即可.(2)
=25,即a3+a5=5,又由a3a5=4,解出q,a1即可.(2)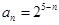 代入
代入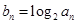 中,得到bn=5-n,即数列,{bn}是以4为首项,-1为公差的等差数列,根据等差数列的前n项和公式求之即可.
中,得到bn=5-n,即数列,{bn}是以4为首项,-1为公差的等差数列,根据等差数列的前n项和公式求之即可.试题解析:解:(1)因为a1a5+2a3a5+a2a8=25,所以,
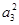 +2a3a5+
+2a3a5+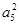 =25
=25又an>o,…a3+a5=5, 3分
又a3与a5的等比中项为2,所以,a3a5=4
而q
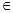 (0,1),所以,a3>a5,所以,a3=4,a5=1,
(0,1),所以,a3>a5,所以,a3=4,a5=1,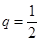 ,a1=16,所以,
,a1=16,所以,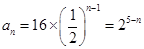 6分
6分(2)bn=log2an=5-n,所以,bn+1-bn=-1,
所以,{bn}是以4为首项,-1为公差的等差数列 8分
所以,
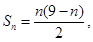 10分
10分
练习册系列答案
相关题目
 为数列
为数列 的前
的前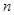 项和,且有
项和,且有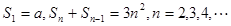
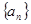 是单调递增数列,求
是单调递增数列,求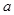 的取值范围.
的取值范围.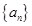 ,等比数列
,等比数列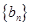 中,
中,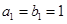 ,
,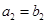 ,
,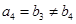 .
.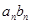 ;
;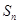 为数列
为数列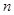 项和,
项和,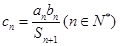 ,
,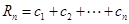 ,求
,求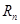 .
.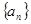 的前
的前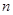 项和
项和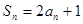 ,求证:
,求证: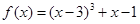 ,数列
,数列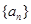 是公差不为0的等差数列,
是公差不为0的等差数列,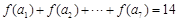 ,则
,则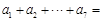 ( )
( )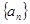 中,如果
中,如果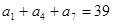 ,
,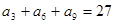 ,则数列
,则数列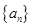 ,满足
,满足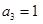 ,
,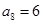 ,则此数列的前
,则此数列的前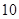 项的和
项的和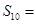 .
. 中,
中,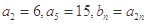 ,则数列
,则数列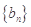 的前5项和
的前5项和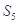 =______.
=______.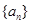 中,已知
中,已知 ,则该数列前11项的和
,则该数列前11项的和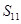 等于( )
等于( )