题目内容
(本题满分15分)已知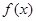 在定义域上是奇函数,且在
在定义域上是奇函数,且在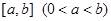 上是减函数,图像如图所示.
上是减函数,图像如图所示.
(1)化简: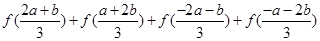 ;
;
(2)画出函数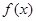 在
在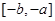 上的图像;
上的图像;
(3)证明: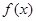 在
在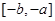 上是减函数.
上是减函数.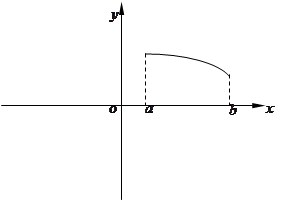
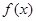 在定义域上是奇函数,且在
在定义域上是奇函数,且在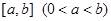 上是减函数,图像如图所示.
上是减函数,图像如图所示.(1)化简:
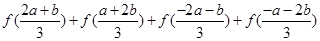 ;
;(2)画出函数
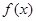 在
在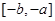 上的图像;
上的图像;(3)证明:
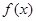 在
在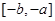 上是减函数.
上是减函数.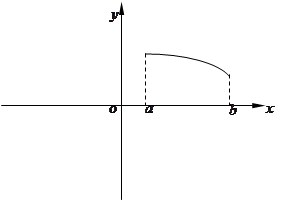
(1)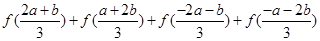

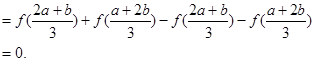 ;
;
(2)图像
(3)函数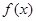 在区间
在区间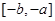 上是减函数.
上是减函数.
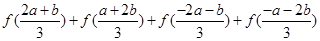

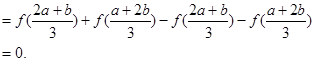 ;
;(2)图像
(3)函数
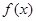 在区间
在区间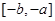 上是减函数.
上是减函数.试题分析:(I)由于f(x)为奇函数,所以f(-x)=-f(x),所以可知
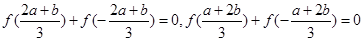 ,因而所求式子的结果为0.
,因而所求式子的结果为0.(II)根据奇函数的图像关于原点对称,直接可画出在对称区间[-b,-a]上的图像.
(III)利用函数的单调性的定义及函数的奇偶性进行证明.
第一步:取值,第二步:作差变形,第三步根据差值符号得到结论.
(1)
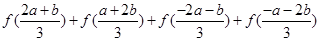

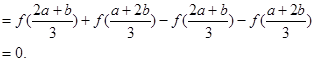 ……
……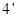
(2)图像……
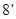
(3)任取
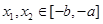 ,且
,且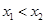 ……
……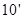
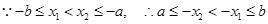 .
.又函数
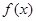 在
在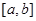 上是减函数,所以
上是减函数,所以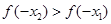 . ……
. ……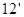
因为
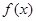 是奇函数,所以
是奇函数,所以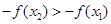 ,即
,即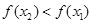 ,
,故函数
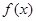 在区间
在区间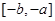 上是减函数. ……
上是减函数. ……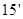 .
.点评:函数的奇偶性一要看定义域是否关于原点对称,二要看f(-x)与f(x)是相等还是互为相反数.奇函数的图像关于原点对称,偶函数的图像关于y轴对称.利用函数的单调性定义证明分三个步骤:一取值,二作差变形,三判断差值符号.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
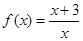 :
: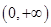 为单调递减函数;
为单调递减函数;  的奇偶性.
的奇偶性.
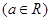 ,
,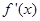 为
为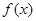 的导数.
的导数.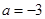 时,求
时,求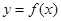 的单调区间和极值;
的单调区间和极值;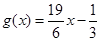 ,是否存在实数
,是否存在实数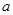 ,对于任意的
,对于任意的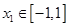 ,存在
,存在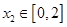 ,使得
,使得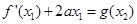 成立?若存在,求出
成立?若存在,求出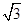 sinxcosx+2cos2x.
sinxcosx+2cos2x.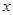 均有
均有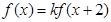 ,其中常数k为负数,且
,其中常数k为负数,且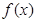 在区间
在区间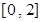 上有表达式
上有表达式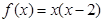
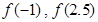 的值;
的值;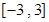 上的表达式,并讨论函数
上的表达式,并讨论函数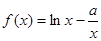 。
。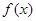 的单调区间;
的单调区间;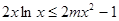 在
在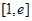 恒成立,求
恒成立,求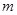 的取值范围。
的取值范围。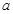 (
(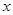 ,绿地面积为
,绿地面积为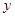 .
.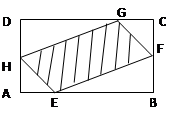
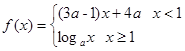 在
在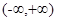 上是减函数,则
上是减函数,则 的取值范围为 .
的取值范围为 .