题目内容
(本小题满分12分)
已知函数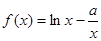 。
。
(Ⅰ)讨论函数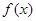 的单调区间;
的单调区间;
(Ⅱ)若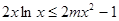 在
在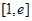 恒成立,求
恒成立,求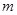 的取值范围。
的取值范围。
已知函数
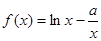 。
。(Ⅰ)讨论函数
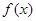 的单调区间;
的单调区间;(Ⅱ)若
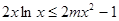 在
在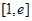 恒成立,求
恒成立,求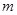 的取值范围。
的取值范围。解:(Ⅰ)当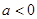 时,
时,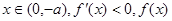 单调递减,
单调递减,
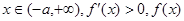 单调递增。
单调递增。
当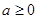 时,
时, 单调递增。
单调递增。
(Ⅱ)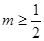 。
。
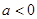 时,
时,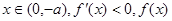 单调递减,
单调递减,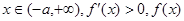 单调递增。
单调递增。当
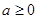 时,
时, 单调递增。
单调递增。(Ⅱ)
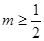 。
。试题分析: (1)因为
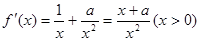 ,然后分母为正,然后确定分子的正负来得到单调区间。
,然后分母为正,然后确定分子的正负来得到单调区间。(2)要证明
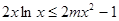 ,得到
,得到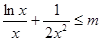
构造函数
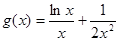 ,求解最大值即可。
,求解最大值即可。解:(Ⅰ)
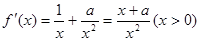
当
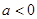 时,
时,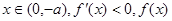 单调递减,
单调递减,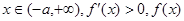 单调递增。
单调递增。当
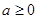 时,
时, 单调递增。
单调递增。(Ⅱ)
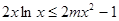 ,得到
,得到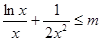
令已知函数
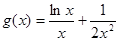

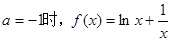
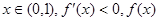 单调递减,
单调递减,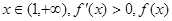 单调递增。
单调递增。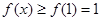 ,即
,即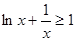 ,
,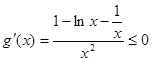
 在
在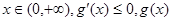 单调递减,
单调递减,在
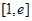 ,
,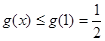 ,若
,若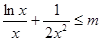 恒成立,则
恒成立,则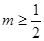 。
。点评:解决该试题的关键是能准确的利用参数的取值范围得到函数的单调性的运用,并且可知函数的最值问题,进而证明不等式的恒成立。

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
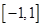 上的偶函数
上的偶函数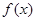 ,已知当
,已知当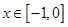 时的解析式
时的解析式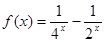
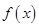 在
在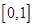 上的解析式;
上的解析式;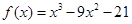 ,且
,且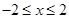 ,则
,则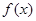 的最大值为 .
的最大值为 .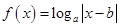 在
在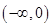 上是增函数,则
上是增函数,则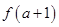 与
与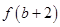 的
的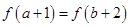
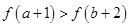
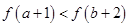
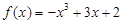 ,若不等式
,若不等式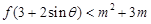 对任意
对任意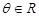
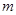 的取值范围为 .
的取值范围为 .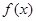 在定义域上是奇函数,且在
在定义域上是奇函数,且在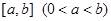 上是减函数,图像如图所示.
上是减函数,图像如图所示.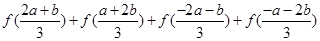 ;
;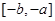 上的图像;
上的图像;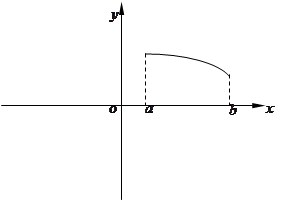
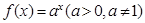 在
在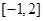 上的最大值为4,最小值为
上的最大值为4,最小值为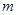 ,
,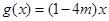 在R上是增函数,则
在R上是增函数,则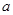 = .
= .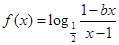 为奇函数,
为奇函数,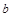 为常数.
为常数.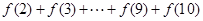 的值;
的值;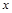 的值,不等式
的值,不等式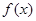 >
>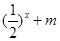 恒成立,求实数
恒成立,求实数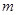 的取值范围.
的取值范围.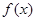 =
=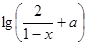 是奇函数,则
是奇函数,则