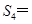题目内容
已知各项均不相等的等差数列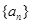 的前四项和
的前四项和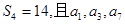 成等比.
成等比.
(1)求数列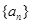 的通项公式;
的通项公式;
(2)设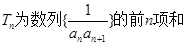 ,若
,若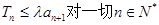 恒成立,求实数
恒成立,求实数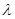 的最大值.
的最大值.
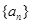 的前四项和
的前四项和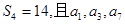 成等比.
成等比.(1)求数列
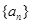 的通项公式;
的通项公式;(2)设
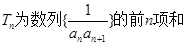 ,若
,若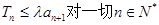 恒成立,求实数
恒成立,求实数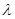 的最大值.
的最大值.(1)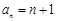 ;(2)
;(2)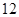
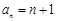 ;(2)
;(2)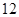
试题分析:数列问题要注意以下两点①等差(比)数列中各有5个基本量,建立方程组可“知三求二”;②数列的本质是定义域为正整数集或其有限子集的函数,数列的通项公式即为相应的解析式,因此在解决数列问题时,应注意用函数的思想求解.(1)由题知,
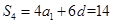 ,又
,又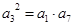 ,利用等差数列通项公式展开,得
,利用等差数列通项公式展开,得 方程,联立求
方程,联立求 ,进而求数列
,进而求数列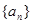 的通项公式;(2)求数列前
的通项公式;(2)求数列前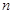 项和,首先考虑其通项公式
项和,首先考虑其通项公式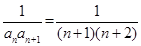 ,利用裂项相消法,求得
,利用裂项相消法,求得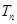 ,再利用参变分离法,转化为求函数的最值问题处理.
,再利用参变分离法,转化为求函数的最值问题处理.试题解析:(1)设公差为d,由已知得:
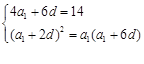 ,联立解得
,联立解得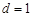 或
或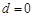 (舍去)
(舍去)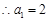 ,故
,故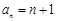 6分
6分(2)
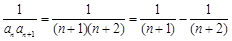 8分
8分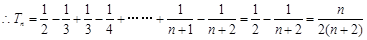 10分
10分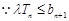 ,
,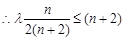 ,
,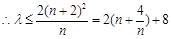
又
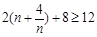 ,
,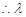 的最大值为12 14分
的最大值为12 14分 项和;3、裂项相消法.
项和;3、裂项相消法.
练习册系列答案
相关题目
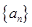 是首项为
是首项为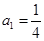 ,公比
,公比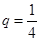 的等比数列,设
的等比数列,设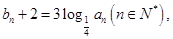 .
.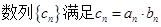
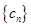 的前n项和
的前n项和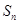 ;
;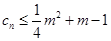 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.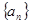 中,
中,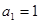 ,
,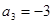 .
.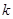 项和
项和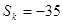 ,求
,求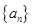 中,
中,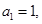 且对任意的
且对任意的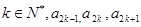 成等比数列,其公比为
成等比数列,其公比为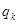 ,
,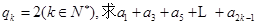 ;
;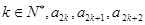 成等差数列,其公差为
成等差数列,其公差为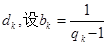 .
.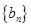 成等差数列,并指出其公差;
成等差数列,并指出其公差;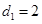 ,试求数列
,试求数列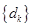 的前
的前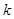 项和
项和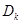 .
.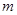 的有穷数列数集
的有穷数列数集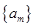 ,记
,记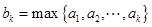
 ,即
,即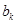 为
为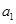 、
、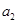 、
、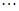 、
、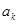 中的最大值,并称数列
中的最大值,并称数列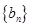 是
是 的控制数列.如
的控制数列.如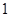 、
、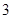 、
、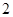 、
、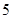 、
、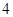 、
、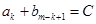 (
(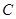 为常数,
为常数,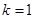 、
、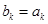
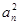 ·bn,证明:当且仅当n≥3时,cn+1<cn..
·bn,证明:当且仅当n≥3时,cn+1<cn..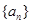 ,若点
,若点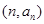
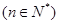 均在直线
均在直线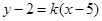 上,则数列
上,则数列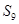 等于( )
等于( )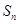 表示数列
表示数列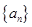 的前
的前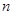 项和,若对任意的
项和,若对任意的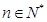 满足
满足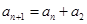 ,且
,且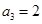 ,则
,则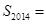 ( )
( )



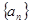 的前
的前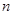 项和为
项和为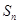 ,若
,若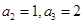 ,则
,则