题目内容
从集合 中随机选取一个数记为
中随机选取一个数记为 ,从集合
,从集合 中随机选取一个数记为b,则函数
中随机选取一个数记为b,则函数
 是增函数的概率为
是增函数的概率为
 中随机选取一个数记为
中随机选取一个数记为 ,从集合
,从集合 中随机选取一个数记为b,则函数
中随机选取一个数记为b,则函数
 是增函数的概率为
是增函数的概率为A. | B. | C. | D. |
D
分析:根据题意,列举a、b全部可能的情况,可得其情况数目,由一次函数的性质分析可得a=1或2时,f(x)=ax+b是增函数,可得其情况数目,进而由古典概型公式,计算可得答案.
解:根据题意,a、b的情况有:
a=-1、b=-1,a=-1、b=0,a=-1、b=2,
a=1、b=1,a=1、b=0,a=1、b=2,
a=2、b=1,a=2、b=0,a=2、b=2,共9种情况;
若函数f(x)=ax+b是增函数,必有a>0,
即a=1或2时,f(x)=ax+b是增函数,其情况有6种,
则函数f(x)=ax+b是增函数的概率为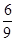 =
=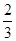 ;
;
故选D.
点评:本题考查古典概型的计算,关键由一次函数的性质分析出f(x)为增函数的条件.
解:根据题意,a、b的情况有:
a=-1、b=-1,a=-1、b=0,a=-1、b=2,
a=1、b=1,a=1、b=0,a=1、b=2,
a=2、b=1,a=2、b=0,a=2、b=2,共9种情况;
若函数f(x)=ax+b是增函数,必有a>0,
即a=1或2时,f(x)=ax+b是增函数,其情况有6种,
则函数f(x)=ax+b是增函数的概率为
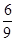 =
=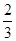 ;
;故选D.
点评:本题考查古典概型的计算,关键由一次函数的性质分析出f(x)为增函数的条件.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 的高二(1)班男同学有
的高二(1)班男同学有 名,女同学有
名,女同学有 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;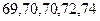 ,第二次做试验的乙同学得
,第二次做试验的乙同学得 到的试验数据为
到的试验数据为 ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由. .
. .
. 的回归直线方程是:
的回归直线方程是: ,使代数式
,使代数式


 的值最小时,
的值最小时, ,
, ,(
,( 、
、 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数) ,即称
,即称 为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率. ,对周一和周二的单词每个能默写对的概率为
,对周一和周二的单词每个能默写对的概率为 ;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数
;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数 的分布列和期望.
的分布列和期望. 的分布列为
的分布列为
 ,则
,则 的值为 ( )
的值为 ( )




 拐入同一公路时,需要有一车等待.已知甲车拐入需要的时间为2分钟,乙车拐入需要的时间为1分钟,倘若甲、乙两车都在某5分
拐入同一公路时,需要有一车等待.已知甲车拐入需要的时间为2分钟,乙车拐入需要的时间为1分钟,倘若甲、乙两车都在某5分 钟内到达转弯路口,则至少有一辆车转弯时需要
钟内到达转弯路口,则至少有一辆车转弯时需要 等待的概率
等待的概率  的距离小于1的概率为 。
的距离小于1的概率为 。 变量X的分布列为
变量X的分布列为
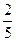
 。
。