题目内容
【题目】某学校400名学生在一次百米赛跑测试中,成绩全部都在12秒到17秒之间,现抽取其中50个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图所示的是按上述分组方法得到的频率分布直方图.
,如图所示的是按上述分组方法得到的频率分布直方图.

(1)请估计该校400名学生中,成绩属于第三组的人数;
(2)请估计样本数据的中位数(精确到0.01);
(3)若样本第一组中只有一名女生,其他都是男生,第五组则只有一名男生,其他都是女生,现从第一、第五组中各抽取2名同学组成一个特色组,设其中男同学的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
【答案】(1)152(2)14.74秒(3)分布列见解析, ![]()
【解析】试题分析:(1)由直方图可知,第三组的概率为0.38,第三组的共有![]() ;(2)中位数落在第三组,设样本中位数为
;(2)中位数落在第三组,设样本中位数为![]() ,根据中位数左右两边的小矩形面积之和相等,解得
,根据中位数左右两边的小矩形面积之和相等,解得![]() ;(3)第一组男生2人,女生1人,第五组男生1人,女生3人,则
;(3)第一组男生2人,女生1人,第五组男生1人,女生3人,则![]() 的可能取值为1,2,3,求出概率,写出分布列,并求出期望。
的可能取值为1,2,3,求出概率,写出分布列,并求出期望。
试题解析:
(1)由频率分布直方图可知,成绩属于第三组的概率为0.38,故可估计该校400名学生成绩属于第三组的共有![]() (人).
(人).
(2)由频率分布直方图易判断,样本数据的中位数落在第三组;设样本中位数为![]() ,根据中位数左右两边的小矩形面积之和相等可得
,根据中位数左右两边的小矩形面积之和相等可得![]() ,解得
,解得![]() (秒).
(秒).
(3)第一组的人数为![]() ,其中男生2人,女生1人,第五组的人数为
,其中男生2人,女生1人,第五组的人数为![]() ,其中1名男生,3名女生,故
,其中1名男生,3名女生,故![]() 的可能取值为1,2,3,
的可能取值为1,2,3,
![]() ,
, ![]() ,
,
![]() ,
,
![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
|
|
|
|
所以![]() .
.

【题目】某学校高三年级有学生750人,其中男生450人,女生300人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分别分为男、女两组,再将两组学生的分数分成5组,分别加以统计,得到如图所示的频率分布直方图.
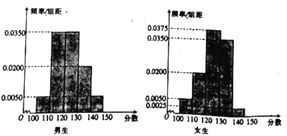
(1)从样本中分数小于110分的学生中随机抽取两人,求两人性别相同的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,试判断能否在犯错误的概率不超过0.1的前提下认为“数学尖子生与性别有关”.
附: 
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】已知x与y之间的几组数据如下表:
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得的线性回归方程为![]() =
=![]() x+
x+![]() .若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
A. ![]() >b′,
>b′,![]() >a′ B.
>a′ B. ![]() >b′,
>b′,![]() <a′
<a′
C. ![]() <b′,
<b′,![]() >a′ D.
>a′ D. ![]() <b′,
<b′,![]() <a′
<a′