题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,且
,且![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,且
,且![]() 在底
在底![]() 内的射影恰为
内的射影恰为![]() 的中点
的中点![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上任意一点.
上任意一点.
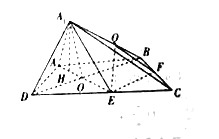
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据![]() 平面ABCD,得到
平面ABCD,得到![]() ,由平面几何知识得到
,由平面几何知识得到![]() ,从而得到
,从而得到![]() 平面
平面![]() ,所以所以平面
,所以所以平面![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点建立空间直角坐标系,得到平面
为原点建立空间直角坐标系,得到平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,得到这两个面所成的锐角二面角的余弦值.
的法向量,利用向量的夹角公式,得到这两个面所成的锐角二面角的余弦值.
(1)由题意,E为CD的中点,
因为![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
所以![]() ,又因为
,又因为![]() ,
,
![]() ,
,![]() ,
,
所以![]() 垂直平分
垂直平分![]() ,
,
所以![]()
又因![]() ,
,![]()
所以![]() 为正方形,
为正方形,
所以![]()
因为![]() 为
为![]() 的中点,
的中点,
所以![]()
而![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)因为![]() 在底面ABCD内的射影恰为OA的中点H,
在底面ABCD内的射影恰为OA的中点H,
所以![]() .
.
因为![]() ,所以过点O分别作AD,AB的平行线(如图),
,所以过点O分别作AD,AB的平行线(如图),
并以它们分别为x,y轴,
以过O点且垂直于![]() 平面的直线为z轴,
平面的直线为z轴,
建立如图所示的空间直角坐标系,
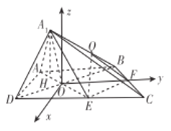
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,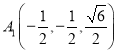 ,
,
所以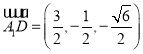 ,
,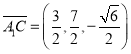 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则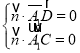 ,所以
,所以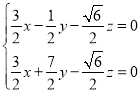
令![]() ,则
,则![]() ,
,
由(1)知,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则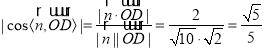 .
.
故平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目