Question

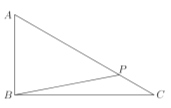
【题目】如图，某公园有三个警卫室、、有直道相连，千米，千米，千米.

（1）保安甲沿从警卫室出发行至点处，此时，求的直线距离；

（2）保安甲沿从警卫室出发前往警卫室，同时保安乙沿从警卫室出发前往警卫室，甲的速度为1千米/小时，乙的速度为2千米/小时，若甲乙两人通过对讲机联系，对讲机在公园内的最大通话距离不超过3千米，试问有多长时间两人不能通话？（精确到0.01小时）

Answer 1

【答案】（1）；（2）.

【解析】

(1)由解直角三角形可得∠C=30°，在△BPC中由余弦定理可得BP的值；（2）设甲出发

后的时间为t小时，则由题意可知0≤t≤4，设甲在线段CA上的位置为点M，则AM=4﹣t，讨论0≤t≤1时，当1≤t≤4时，分别在△AMQ和△AMB中，运用余弦定理和二次不等式的解法，即可得到所求结论．

（1）在Rt△ABC中，AB=2，BC=2，

所以∠C=30°，

在△PBC中PC=1，BC=2，

由余弦定理可得

BP2=BC2+PC2﹣2BCPCcos30°

=（2）2+1﹣2×2×1×=7，

即BP=；

（2）在Rt△ABC中，BA=2，BC=2，AC=4，

设甲出发后的时间为t小时，则由题意可知0≤t≤4，

设甲在线段CA上的位置为点M，则AM=4﹣t，

①当0≤t≤1时，设乙在线段AB上的位置为点Q，则AQ=2t，

如图所示，在△AMQ中，

由余弦定理得MQ2=（4﹣t）2+（2t）2﹣22t（4﹣t）cos60°=7t2﹣16t+16＞9，

解得t＜或t＞，

所以0≤t≤；

②当1≤t≤4时，乙在警卫室B处，在△ABM中，

由余弦定理得MB2=（4﹣t）2+4﹣22t（4﹣t）cos60°=t2﹣6t+12＞9，

解得t＜3﹣或t＞3+，又1≤t≤4，不合题意舍去．

综上所述0≤t≤时，甲乙间的距离大于3千米，

所以两人不能通话的时间为小时．