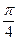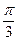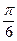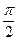题目内容
设n和m是两个单位向量,其夹角是60°,求向量a=2m+n与b=2n-3m的夹角.
a,b夹角为120°
由|m|=1,|n|=1,夹角为60°,得m·n=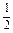 .
.
则有|a|=|2m+n|=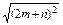 =
=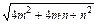 =
=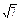 .
.
|b|=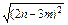 =
=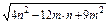 =
=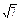 .
.
而a·b=(2m+n)·(2n-3m)=m·n-6m2+2n2=-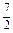 ,
,
设a与b的夹角为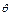 ,
,
则cos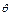 =
=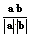 =
=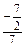 =-
=-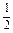 .故a,b夹角为120°.
.故a,b夹角为120°.
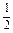 .
.则有|a|=|2m+n|=
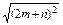 =
=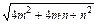 =
=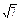 .
.|b|=
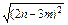 =
=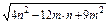 =
=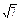 .
.而a·b=(2m+n)·(2n-3m)=m·n-6m2+2n2=-
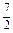 ,
,设a与b的夹角为
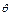 ,
,则cos
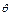 =
=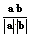 =
=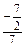 =-
=-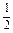 .故a,b夹角为120°.
.故a,b夹角为120°.
练习册系列答案
相关题目
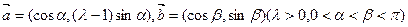 是平面上的两个向量,且
是平面上的两个向量,且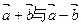 互相垂直.
互相垂直.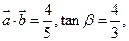 求
求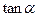 的值.
的值. 中,角
中,角 所对的边分别为
所对的边分别为 ,
, ,
,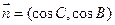 ,且
,且
 .(I)求
.(I)求 ;(
;( II)若
II)若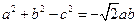 ,且
,且 ,求
,求 .
.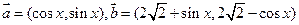 ,
,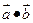 ,
,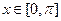 (1)求f(x)的值域;(2)若
(1)求f(x)的值域;(2)若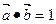 ,求
,求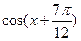 的值
的值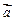 与
与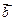 的夹角为30°,且|
的夹角为30°,且|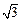 ,|
,|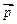 =
=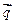 =
=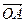 =(1,7),
=(1,7),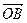 =(5,1),
=(5,1),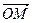 =(2,1),点P是直线OM上的一个动点,求当
=(2,1),点P是直线OM上的一个动点,求当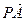 ·
·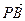 取最小值时,
取最小值时,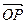 的坐标及ÐAPB的余弦值.
的坐标及ÐAPB的余弦值. 的夹角为 ,
的夹角为 , ,则
,则
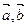 满足
满足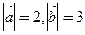 ,且
,且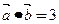 ,则
,则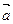 与
与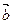 的夹角为
的夹角为