题目内容
(12分)设平面内的向量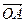 =(1,7),
=(1,7),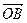 =(5,1),
=(5,1),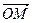 =(2,1),点P是直线OM上的一个动点,求当
=(2,1),点P是直线OM上的一个动点,求当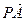 ·
·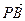 取最小值时,
取最小值时,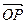 的坐标及ÐAPB的余弦值.
的坐标及ÐAPB的余弦值.
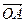 =(1,7),
=(1,7),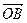 =(5,1),
=(5,1),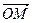 =(2,1),点P是直线OM上的一个动点,求当
=(2,1),点P是直线OM上的一个动点,求当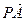 ·
·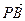 取最小值时,
取最小值时,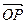 的坐标及ÐAPB的余弦值.
的坐标及ÐAPB的余弦值. -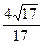
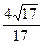
设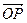 =(x,y),。∵点P在直线OM上,∴
=(x,y),。∵点P在直线OM上,∴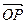 与
与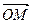 共线,而
共线,而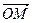 =(2,1),
=(2,1),
∴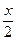 =
=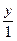 ,即x=2y,则有
,即x=2y,则有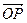 =(2y,y),∵
=(2y,y),∵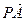 =
=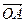 -
-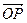 =(1,7)-(2y,y)=(1-2y,7-y),
=(1,7)-(2y,y)=(1-2y,7-y),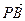 =
=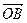 -
-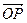 =(5,1)-(2y,y)=(5-2y,1-y),
=(5,1)-(2y,y)=(5-2y,1-y),
∴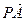 ·
·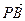 =(1-2y,7-y)·(5-2y,1-y)=(1-2y)(5-2y)+(7-y)(1-y)
=(1-2y,7-y)·(5-2y,1-y)=(1-2y)(5-2y)+(7-y)(1-y)
=5y2-20y+12=5(y-2)2-8,从而,当 且仅当y=2,x=4时,
且仅当y=2,x=4时,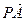 ·
·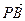 取得最小值-8,此时
取得最小值-8,此时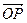 =(4,2),
=(4,2),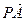 =(-3,5),
=(-3,5),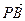 =(1,
=(1, -1),
-1),
于是此时|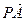 |=
|=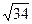 ,|
,|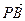 |=
|=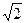 ,
,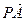 ·
·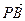 =-8,
=-8,
∴cosÐAPB=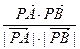 =
=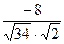 =-
=-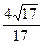 .
.
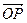 =(x,y),。∵点P在直线OM上,∴
=(x,y),。∵点P在直线OM上,∴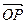 与
与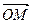 共线,而
共线,而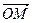 =(2,1),
=(2,1), ∴
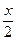 =
=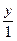 ,即x=2y,则有
,即x=2y,则有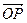 =(2y,y),∵
=(2y,y),∵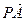 =
=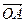 -
-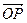 =(1,7)-(2y,y)=(1-2y,7-y),
=(1,7)-(2y,y)=(1-2y,7-y),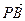 =
=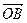 -
-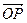 =(5,1)-(2y,y)=(5-2y,1-y),
=(5,1)-(2y,y)=(5-2y,1-y),∴
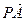 ·
·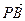 =(1-2y,7-y)·(5-2y,1-y)=(1-2y)(5-2y)+(7-y)(1-y)
=(1-2y,7-y)·(5-2y,1-y)=(1-2y)(5-2y)+(7-y)(1-y)=5y2-20y+12=5(y-2)2-8,从而,当
 且仅当y=2,x=4时,
且仅当y=2,x=4时,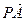 ·
·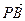 取得最小值-8,此时
取得最小值-8,此时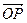 =(4,2),
=(4,2),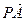 =(-3,5),
=(-3,5),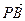 =(1,
=(1, -1),
-1),于是此时|
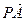 |=
|=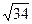 ,|
,|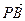 |=
|=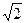 ,
,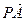 ·
·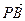 =-8,
=-8, ∴cosÐAPB=
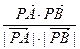 =
=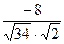 =-
=-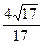 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
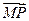 ·
·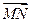 ,
,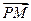 ·
·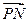 ,
,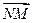 ·
·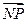 成公差小于零的等差数列(1)点P的轨迹是什么曲线?(2)若点P坐标为(
成公差小于零的等差数列(1)点P的轨迹是什么曲线?(2)若点P坐标为(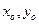 ),记
),记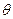 为
为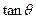 ;
;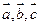 是任意的非零向量,且相互不共线,则(1)
是任意的非零向量,且相互不共线,则(1)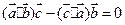 ;(2)
;(2)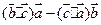 不与
不与 垂直;(3)
垂直;(3)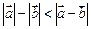 ;(4)
;(4)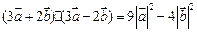 中,是真命题的有 ( )
中,是真命题的有 ( )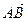 =
=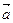 ,
,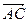 =
=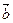 ,
,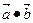 <0,
<0,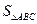 =
=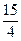 ,
,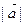 =3,
=3,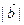 =5,则
=5,则 夹角为 ( )
夹角为 ( )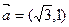 ,向量
,向量 .
.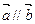 ,且
,且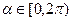 ,将
,将 表示为
表示为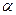 的函数,并求
的函数,并求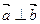 ,且
,且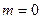 , 求
, 求 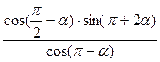 的值.
的值. 分别是与
分别是与 向的单位向量,则下列结论中正确的是( )
向的单位向量,则下列结论中正确的是( )



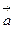
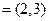 ,
,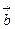
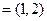 ,若向量
,若向量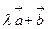 与向量
与向量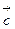
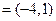 垂直,则λ= .
垂直,则λ= .