题目内容
若两个正实数x，y满足
＋
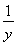＝1，并且x＋2y＞m2＋2m恒成立，则实数m的取值范围是( )
A．(－∞，－2)∪[4，＋∞) B．(－∞，－4]∪[2，＋∞)
C．(－2,4) D．(－4,2)
D
【解析】x＋2y＝(x＋2y)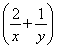 
＝2＋
＋2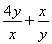≥8，当且仅当
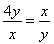，即4y2＝x2时等号成立．x＋2y＞m2＋2m恒成立，则m2＋2m＜8，m2＋2m－8＜0，解得－4＜m＜2，故选D.
练习册系列答案
相关题目
题目内容
若两个正实数x，y满足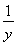＋＝1，并且x＋2y＞m2＋2m恒成立，则实数m的取值范围是( )
A．(－∞，－2)∪[4，＋∞) B．(－∞，－4]∪[2，＋∞)
C．(－2,4) D．(－4,2)
D
【解析】x＋2y＝(x＋2y) 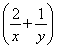＝2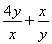＋＋2≥8，当且仅当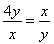，即4y2＝x2时等号成立．x＋2y＞m2＋2m恒成立，则m2＋2m＜8，m2＋2m－8＜0，解得－4＜m＜2，故选D.
