题目内容
12．已知x1、x2是方程x2+（2-m）x+（1+m）=0的两个根，求x12+x22的最小值．分析 由题意和韦达定理可得m≤0或m≥8，且x12+x22=（m-4）2-16，由二次函数的单调性和最值可得．
解答 解：∵x1、x2是方程x2+（2-m）x+（1+m）=0的两个根，
∴x1+x2=m-2，x1x2=1+m，且△=（2-m）2-4（1+m）≥0，
∴x12+x22=（x1+x2）2-4x1x2=（m-2）2-4（1+m）
=m2-8m=（m-4）2-16，
解不等式△=（2-m）2-4（1+m）≥0可得m≤0或m≥8，
由二次函数单调性可知y=（m-4）2-16在（-∞，0]单调递减，在[8，+∞）单调递增，
当x=0时，y=0，当x=8时，y=0，
∴x12+x22的最小值为0
点评 本题考查不等式的解法即式子的最值，涉及二次函数的单调性和最值以及韦达定理，属基础题．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
20．若a，b，c∈（0，+∞），且a+b+c=1，则$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$的最小值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{\root{3}{2}}{3}$ | C． | $\frac{9}{2}$ | D． | $\frac{1}{9}$ |
17．$cos（\frac{19π}{3}）$的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $-\frac{1}{2}$ | D． | $-\frac{{\sqrt{3}}}{2}$ |
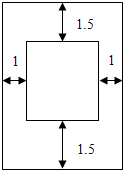某出版社出版一读物，为了排版设计的需要，规定：一页上所印文字的矩形区域需要占去150cm2，上、下边各要留1.5cm宽的空白，左、右两边各要留1cm宽的空白，出版商为了节约纸张，应选用怎样尺寸的矩形纸张来设计版面？
2．不等式（3x+1）（2x-1）＞0的解集是（ ）
| A． | $\{x|x＜-\frac{1}{3}或x＞\frac{1}{2}\}$ | B． | $\{x|-\frac{1}{3}＜x＜\frac{1}{2}\}$ | C． | $\{x|x＞\frac{1}{2}\}$ | D． | $\{x|x＞-\frac{1}{3}\}$ |