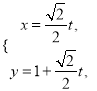题目内容
【题目】在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，已知点A的极坐标为（ 
， 
），直线l的极坐标方程为ρcos（θ﹣ ）=a，且点A在直线l上，
（1）求a的值及直线l的直角坐标方程；
（2）圆C的参数方程为 
（α为参数），试判断直线l与圆C的位置关系．
【答案】
（1）解：点A（ 
， 
）在直线l上，得 cos（θ﹣ ）=a，∴a= ，
故直线l的方程可化为：ρsinθ+ρcosθ=2，
得直线l的直角坐标方程为x+y﹣2=0
（2）解：消去参数α，得圆C的普通方程为（x﹣1）2+y2=1
圆心C到直线l的距离d= 
＜1，
所以直线l和⊙C相交
【解析】（1）根据点A在直线l上，将点的极坐标代入直线的极坐标方程即可得出a值，再利用极坐标转化成直角坐标的转换公式求出直线l的直角坐标方程；（2）欲判断直线l和圆C的位置关系，只需求圆心到直线的距离与半径进行比较即可，根据点到线的距离公式求出圆心到直线的距离然后与半径比较．
练习册系列答案
相关题目
