题目内容
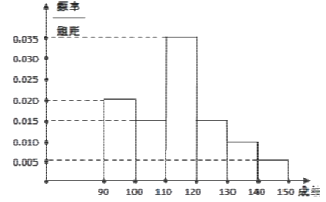
【题目】某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人. 
(1)请补充完整频率分布直方图,并估计这组数据的平均数M;
(2)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为x,y.若|x﹣y|≥10,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率P1;
(3)以此样本的频率当作概率,现随机在这组样本中选出3名学生,求成绩不低于120分的人数ξ的分布列及期望.
【答案】
(1)解:频率分布直方图见解析,
M=95×0.2+105×0.15+115×0.35+125×0.15+135×0.1+145×0.05=114.5
(2)解:依题意可得:第四组人数为:
![]() =12,
=12,
故P1= ![]() =
= ![]()
(3)解:依题意可得:样本总人数为: ![]() =80,成绩不低于120分的人数为:80×(0.05+0.10+0.15)=24,故在样本中任选1人,其成绩不低于120分的概率=
=80,成绩不低于120分的人数为:80×(0.05+0.10+0.15)=24,故在样本中任选1人,其成绩不低于120分的概率= ![]() =
= ![]() .由已知ξ的可能取值为0,1,2,3.
.由已知ξ的可能取值为0,1,2,3.
ξ~B ![]() ,P(ξ=0)=
,P(ξ=0)= ![]() =
= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() .ξ的分布列如下
.ξ的分布列如下
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
故Eξ= ![]() =
= ![]() .
.
【解析】(1)利用频率分布直方图的性质即可得出.(2)依题意可得:第四组人数为: ![]() =12,可得P1=
=12,可得P1= ![]() .(3)依题意可得:样本总人数为:
.(3)依题意可得:样本总人数为: ![]() =80,成绩不低于120分的人数为:80×(0.05+0.10+0.15)=24,故在样本中任选1人,其成绩不低于120分的概率=
=80,成绩不低于120分的人数为:80×(0.05+0.10+0.15)=24,故在样本中任选1人,其成绩不低于120分的概率= ![]() =
= ![]() .由已知ξ的可能取值为0,1,2,3.ξ~B
.由已知ξ的可能取值为0,1,2,3.ξ~B ![]() ,即可得出.
,即可得出.
【考点精析】通过灵活运用频率分布直方图,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息即可以解答此题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案