题目内容
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人. 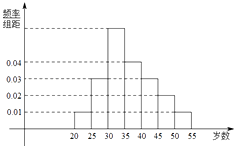
(1)求N和[30,35)这组的参加者人数N1;
(2)已知[30,35)和[35,40)这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有1名数学老师的概率;
(3)组织者从[45,55)这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为x,求x的分布列和均值.
【答案】
(1)解:∵年龄在[35,40)内的频率为0.04×5=0.2,
∴总人数N= ![]() =40人.
=40人.
∵[30,35)这组的频率为:1﹣(0.01×2+0.02+0.03×2+0.04)×5=0.3,
[30,35)这组的参加者人数N1为:40×0.3=12人
(2)解:记事件B为“从年龄在[30,35]之间选出的人中至少有2名数学教师”,
∵年龄在[30,35)之间的人数为12,
∴P(B)=1﹣ ![]() =
= ![]() ,
,
记事件C为“从年龄在[35,40)之间选出的人中至少有1名数学教师”,
∵年龄在[35,40)之间的人数为8,
∴P(C)=1﹣ ![]() =
= ![]() ,
,
∴两组选出的人中都至少有1名数学老师的概率P(BC)= ![]() =
= ![]()
(3)解:年龄在[45,55)之间的人数为6人,其中女教师4人,
∴ξ的可能取值为1,2,3,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() ,
,
∴ξ的分布列为:
ξ | 1 | 2 | 3 |
P |
|
|
|
Eξ= ![]() =2
=2
【解析】(1)先求出年龄在[35,40)内的频率,由此能求出总人数和[30,35)这组的参加者人数N1 . (2)记事件B为“从年龄在[30,35]之间选出的人中至少有1名数学教师”,记事件C为“从年龄在[35,40)之间选出的人中至少有1名数学教师”,分别求出P(B),P(C),由此能求出两组选出的人中都至少有1名数学老师的概率.(3)年龄在[45,55)之间的人数为6人,其中女教师4人,ξ的可能取值为1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
【考点精析】本题主要考查了频率分布直方图和离散型随机变量及其分布列的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案