题目内容
【题目】设椭圆
(
)的左、右焦点分别为
，过
的直线交椭圆于
，
两点，若椭圆
的离心率为
，
的周长为
.
(1)求椭圆的方程；
(2)设不经过椭圆的中心而平行于弦
的直线交椭圆于点
，
，设弦，
的中点分别为
，证明：
三点共线.
【答案】(Ⅰ) 
(Ⅱ)详见解析
【解析】
(Ⅰ)由
的周长为
求得
，由离心率求得
，从而可得
的值，进而可得结果；(Ⅱ)易知，当直线
的斜率不存在时，
三点共线；当直线
的斜率存在时，由点差法可得 
，
，即
，
.同理可得
，从而可得结论.
(Ⅰ)由题意知，
.
又∵
，∴
，
，
∴椭圆
的方程为.
(Ⅱ)易知，当直线的斜率不存在时，由椭圆的对称性知，中点
在
轴上，三点共线；
当直线的斜率存在时，设其斜率为
，且设
.
联立方程得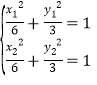
相减得
，
∴
，
∴，，即，
∴.
同理可得，∴
，所以三点共线.
走进文言文系列答案
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
(单位：千元)对年销售量
(单位：
)和年利润
(单位：千元)的影响.对近
年的年宣传费
和年销售量数据
作了初步处理，得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.附：对于一组数据
，
，
，
，其回归直线
的斜率和截距的最小二乘法估计分别为
，
.
（1）根据散点图判断，
与
在哪一个适宜作为年销售量 关于年宣传费 的回归方程类型？(给出判断即可，不必说明理由)
（2）根据1小问的判断结果及表中数据，建立 关于 的回归方程；
（3）已知这种产品的年利润 与
的关系为
.根据2小问的结果回答下列问题：
①2年宣传费
时，年销售量及年利润的预报值是多少？
②3年宣传费为何值时，年利润的预报值最大？
【题目】（本小题满分12分）
某学校用简单随机抽样方法抽取了100名同学，对其日均课外阅读时间（单位：分钟）进行调查，结果如下：
t |
|
|
|
|
|
|
男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.
（1）将频率视为概率，估计该校4000名学生中“读书迷”有多少人？
（2）从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
（i）求抽取的4位同学中既有男同学又有女同学的概率；
（ii）记抽取的“读书迷”中男生人数为
，求
的分布列和数学期望
