Question

【题目】已知函数，若方程有四个不等实根，时，不等式恒成立，则实数的最小值为（）

A. B. C. D.

Answer 1

【答案】C

【解析】

画出函数f（x）的图象，结合对数函数的图象和性质，可得x1x2＝1，x1+x22，（4﹣x3）（4﹣x4）＝1，且x1+x2+x3+x4＝8，则不等式kx3x4+x12+x22≥k+11恒成立，可化为：k恒成立，求出的最大值，可得k的范围，进而得到实数k的最小值．

函数f（x）的图象如下图所示：

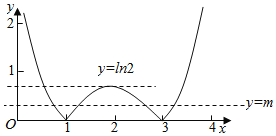
当方程f（x）＝m有四个不等实根x1，x2，x3，x4（x1＜x2＜x3＜x4）时，

|lnx1|＝|lnx2|，即x1x2＝1，x1+x22，

|ln（4﹣x3）|＝|ln（4﹣x4）|，即（4﹣x3）（4﹣x4）＝1，

且x1+x2+x3+x4＝8，

若不等式kx3x4+x12+x22≥k+11恒成立，

则k恒成立，

由[（x1+x2）﹣48]≤2

故k≥2，

故实数k的最小值为2，

故选：C．