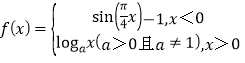Question

【题目】已知函数，其中为常数.

（1）若不等式的解集是,求此时的解析式；

（2）在（1）的条件下，设函数，若在区间上是单调递增函数，求实数的取值范围；

（3）是否存在实数使得函数在上的最大值是？若存在，求出的值；若不存在，请说明理由.

Answer 1

【答案】（1）（2）（3）存在，或

【解析】

（1）根据一元二次不等式与一元二次方程的关系，利用韦达定理，即可求解；

（2）根据二次函数图像确定对称轴和区间的关系，即可求解；

（3）由二次函数图像，求出函数可能取到的最大值，建立方程，求出参数，回代验证；或由对称轴，分类讨论，确定二次函数图象开口方向，函数在上的单调性，求出最大值且等于4，建立方程，即可求得结论.

解：(1)由题意得：是的根

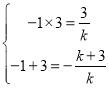∵， 解得

∴

(2)由（1）可得 ，

其对称轴方程为

若在上为增函数，则，解得

综上可知，的取值范围为

(3)当时，

，函数在上的最大值是15，不满足条件

当时，假设存在满足条件的，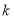

则的最大值只可能在对称轴处取得，

其中对称轴

① 若，则有 ，

的值不存在，

② 若，则，

解得，此时，对称轴，

则最大值应在处取得，与条件矛盾，舍去

③ 若，

则：，且，

化简得，

解得或 ，满足

综上可知，当或时，

函数在上的最大值是4.

(3)另解：当时，

，函数在上的最大值是15，不满足条件

所以，此时的对称轴为

若，，此时

在上最大值为，

解得，与假设矛盾，舍去；

若

①当，即，函数在为增，

在上最大值为

，解得，矛盾舍去

②当，即，矛盾舍…

③当.即，

在上最大值为，

则 ，化简得，

解得或 ，满足 …

综上可知，当或时，

函数在上的最大值是4