题目内容
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 过点
过点![]() ,且椭圆
,且椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)根据题中条件运用基本量之间的关系求解;(2)借助题设条件运用直线和椭圆的位置关系建立坐标之间的关系,再用坐标之间的关系分析推证即可.
试题解析:(1)解:∵椭圆![]() 过点
过点![]() ,∴
,∴![]() ,①………………………………1分
,①………………………………1分
∵椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点,∴
对称的图形过坐标原点,∴![]() ,………………………………2分
,………………………………2分
∵![]() ,∴
,∴![]() ,②…………………………………………………………3分
,②…………………………………………………………3分
由①②得![]() ,
,![]() ,……………………………………………………4分
,……………………………………………………4分
∴椭圆![]() 的方程为
的方程为![]() .………………………………………………5分
.………………………………………………5分
(2)证明:易知直线![]() 的斜率必存在,设直线
的斜率必存在,设直线![]() 的方程为
的方程为![]() ,
,
代入![]() 得
得![]() ,
,
由![]() 得,
得,![]() .…………………………7分
.…………………………7分
设![]() ,
,![]() ,则
,则
![]() ,
,![]() ,……………………………………8分
,……………………………………8分
则直线![]() 的方程为
的方程为![]() ,
,
令![]() 得:
得:![]()
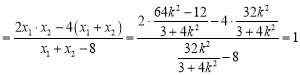 ,
,
∴直线![]() 过定点
过定点![]() ,又
,又![]() 的右焦点为
的右焦点为![]() ,∴直线
,∴直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .…………12分
.…………12分

练习册系列答案
相关题目