题目内容
【题目】已知![]() ,
, ![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)详见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)由函数的解析式可得![]()
![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,由导函数的符号可知
时,由导函数的符号可知![]() 在
在![]() 单调递减;在
单调递减;在![]() 单调递增.
单调递增.
(Ⅱ)构造函数![]() ,问题转化为
,问题转化为![]() 在
在![]() 上恒成立,求导有
上恒成立,求导有![]() ,注意到
,注意到![]() .分类讨论:当
.分类讨论:当![]() 时,不满足题意. 当
时,不满足题意. 当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增;所以
上单调递增;所以![]() ,满足题意.
,满足题意.
则实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)![]()
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() .∴
.∴![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以![]() 在
在![]() 单调递减;在
单调递减;在![]() 单调递增.
单调递增.
(Ⅱ)令![]() ,
,
问题转化为![]() 在
在![]() 上恒成立,
上恒成立,
![]() ,注意到
,注意到![]() .
.
当![]() 时,
时, ![]() ,
,
![]() ,
,
因为![]() ,所以
,所以![]() ,
, ![]() ,
,
所以存在![]() ,使
,使![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 递减,
递减,
所以![]() ,不满足题意.
,不满足题意.
当![]() 时,
时, ![]()
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() 在
在![]() 上单调递增;所以
上单调递增;所以![]() ,满足题意.
,满足题意.
综上所述: ![]() .
.

练习册系列答案
相关题目
【题目】某地![]() 户家庭的年收入
户家庭的年收入![]() (万元)和年饮食支出
(万元)和年饮食支出![]() (万元)的统计资料如下表:
(万元)的统计资料如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;(结果保留到小数点后
的线性回归方程;(结果保留到小数点后![]() 为数字)
为数字)
(2)利用(1)中的回归方程,分析这![]() 户家庭的年饮食支出的变化情况,并预测该地年收入
户家庭的年饮食支出的变化情况,并预测该地年收入![]() 万元的家庭的年饮食支出.(结果保留到小数点后
万元的家庭的年饮食支出.(结果保留到小数点后![]() 位数字)
位数字)
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
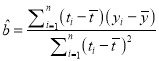 ,
, ![]()
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站.甲、乙乘坐不超过
站.甲、乙乘坐不超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() ;甲、乙乘坐超过
;甲、乙乘坐超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() .
.
(1)求甲、乙两人付费相同的概率;
(2)设甲、乙两人所付费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.