题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过焦点且垂直于
,过焦点且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 所截得的弦长为
所截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
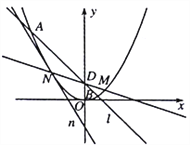
(2)若经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 是坐标原点,求
是坐标原点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据离心率以及弦长,结合![]() ,可知
,可知![]() ,可得结果.
,可得结果.
(2)假设点![]() 坐标,根据斜率存在与否假设直线方程,并与椭圆方程联立,使用韦达定理,表示出
坐标,根据斜率存在与否假设直线方程,并与椭圆方程联立,使用韦达定理,表示出![]() ,结合不等式,可得结果.
,结合不等式,可得结果.
解:(1)设椭圆![]() 的半焦距为
的半焦距为![]() .
.
因为过焦点且垂直于![]() 轴的直线交椭圆
轴的直线交椭圆
![]() 所得的弦长为
所得的弦长为![]() ,所以
,所以![]() ,
,
得![]() ①因为椭圆
①因为椭圆![]() 的离心率为
的离心率为![]() ,
,
所以![]() ②
②
又![]() ③
③
由①②③,解得![]() .
.
故椭圆![]() 的标准方程是
的标准方程是![]() .
.
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,
直线![]() 的方程为
的方程为![]() ,联立
,联立
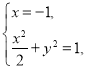 解得
解得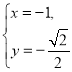 或
或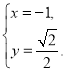
则点![]() 的坐标分别为
的坐标分别为
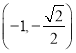 ,
,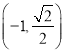 或
或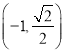 ,
,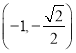 .
.
所以
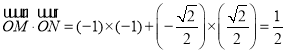 ;
;
当直线![]() 的斜率存在时,
的斜率存在时,
设直线![]() 的方程为
的方程为![]() .
.
联立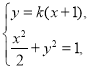 消去
消去![]()
得![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 的内部,
的内部,
所以直线![]() 与椭圆
与椭圆![]() 一定有两个不同的交点
一定有两个不同的交点![]() .
.
则![]() .
.
所以![]()
化简可得![]()
则![]()
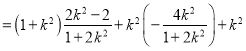
化简可得![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以![]() ,
,
即![]() ,所以
,所以![]() .
.
综上,![]() 的取值范围是
的取值范围是![]() .
.

【题目】某电视台举行文艺比赛,并通过网络对比赛进行直播.比赛现场有5名专家评委给每位参赛选手评分,场外观众可以通过网络给每位参赛选手评分.每位选手的最终得分由专家评分和观众评分确定.某选手参与比赛后,现场专家评分情况如表;场外有数万名观众参与评分,将评分按照[7,8),[8,9),[9,10]分组,绘成频率分布直方图如图:
专家 | A | B | C | D | E |
评分 | 9.6 | 9.5 | 9.6 | 8.9 | 9.7 |
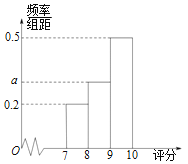
(1)求a的值,并用频率估计概率,估计某场外观众评分不小于9的概率;
(2)从5名专家中随机选取3人,X表示评分不小于9分的人数;从场外观众中随机选取3人,用频率估计概率,Y表示评分不小于9分的人数;试求E(X)与E(Y)的值;
(3)考虑以下两种方案来确定该选手的最终得分:方案一:用所有专家与观众的评分的平均数![]() 作为该选手的最终得分,方案二:分别计算专家评分的平均数
作为该选手的最终得分,方案二:分别计算专家评分的平均数![]() 和观众评分的平均数
和观众评分的平均数![]() ,用
,用![]() 作为该选手最终得分.请直接写出
作为该选手最终得分.请直接写出![]() 与
与![]() 的大小关系.
的大小关系.