Question

【题目】已知椭圆C：+=1（a＞b＞0）的离心率为，且过点（1，）．

（I）求椭圆C的方程；

（Ⅱ）设与圆O：x2+y2=相切的直线l交椭圆C与A，B两点，求△OAB面积的最大值，及取得最大值时直线l的方程．

Answer 1

【答案】（I）（Ⅱ）△OAB面积的最大值为，此时直线方程

【解析】

试题分析：（1）运用椭圆的离心率公式和点满足椭圆方程，解方程可得a，b，进而得到椭圆方程；（2）讨论①当k不存在时，②当k存在时，设直线为y=kx+m，A，B，将直线y=kx+m代入椭圆方程，运用韦达定理和弦长公式，以及直线和圆相切的条件：d=r，结合基本不等式即可得到所求面积的最大值和直线l的方程

试题解析：（1）由题意可得，e==，a2﹣b2=c2，点（1，）代入椭圆方程，可得

+=1，解得a=，b=1，即有椭圆的方程为；

（2）①当k不存在时，x=±时，可得y=±，S△OAB=××=；

②当k存在时，设直线为y=kx+m，A（x1，y1），B（x2，y2），

将直线y=kx+m代入椭圆方程可得（1+3k2）x2+6kmx+3m2﹣3=0，

x1+x2=﹣，x1x2=，

由直线l与圆O：x2+y2=相切，可得=，即有4m2=3（1+k2），

|AB|==

==

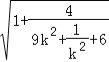=≤=2，

当且仅当9k2= 即k=±时等号成立，可得S△OAB=|AB|r≤×2×=，

即有△OAB面积的最大值为，此时直线方程y=±x±1．