题目内容
【题目】如图，四棱锥P﹣ABCD的底面ABCD为直角梯形，AD‖BC，且 
，BC⊥DC，∠BAD=60°，平面PAD⊥底面ABCD，E为AD的中点，△PAD为等边三角形，M是棱PC上的一点，设 
（M与C不重合）． 
（1）求证：CD⊥DP；
（2）若PA∥平面BME，求k的值；
（3）若二面角M﹣BE﹣A的平面角为150°，求k的值．
【答案】
（1）证明：因为△PAD为等边三角形，E为AD的中点，所以PE⊥AD．
因为平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，PE平面PAD，
所以PE⊥平面ABCD．
又CD平面ABCD，所以PE⊥CD．
由已知得CD⊥DA，PE∩AD=E，所以CD⊥平面PAD．
双DP平面PAD，所以CD⊥DP．
（2）解：连接AC交BE于N，连接MN．
因为PA∥平面BME，PA平面PAC，
平面PAC∩平面BME=MN，所以PA∥MN．
因为 AD∥BC，BC⊥DC，所以∠CBN=∠AEN=90°．
又CB=AE，∠CNB=∠ANE，所以△CNB≌△ANE．
所以CN=NA，则M为PC的中点，k=1．
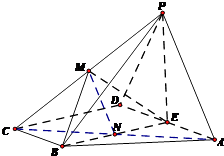
（3）解：方法一：
依题意，若二面角M﹣BE﹣A的大小为150°，则二面角M﹣BE﹣C的大小为30°．
连接CE，过点M作MF∥PE交CE于F，过A（0，1，0）作FG⊥BE于G，连接MG．
因为PE⊥平面ABCD，所以MF⊥平面ABCD．
又BE平面ABCD，所以MF⊥BE．
又MF∩FG=F，MF平面MFG，FG平面MFG，
所以BE⊥平面MFG，从而BE⊥MG．
则∠MGF为二面角M﹣BE﹣C的平面角，即∠MGF=30°．
在等边△PAD中， 
．由于 
，所以 
．
又 
，所以 
．
在△MFG中， 
解得k=3．
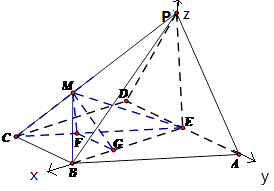
方法二：由于EP⊥EA，EP⊥EB，EA⊥EB，以E为原点，
射线EB，EA，EP分别为x正半轴，y正半轴，z正半轴建立空间直角坐标系，
如图．∵ 
，∠BAD=60°，
∴A（0，1，0）， 
， 
，D（0，﹣1，0），E（0，0，0）， 
平面ABE即xoy平面的一个法向量为 
=（0，0，1）．
设M（x，y，z），由条件 
可知： 
（k＞0），
即 
，
∴ 
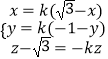，解得：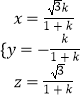 
即 
， 
．
设平面MBE的一个法向量为 
=（x'，y'，z'），
则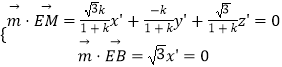 
，x'=0，令 
，则z'=k．即 =（0， 
）．
因为二面角M﹣BE﹣A的平面角为150°，
所以|cos＜ 
＞|=|cos150°|，即 
= 
= 
，
解得k=±3．
因为k＞0，所以k=3．
【解析】（1）推导出PE⊥AD，从而PE⊥平面ABCD，进而PE⊥CD，再由CD⊥DA，得CD⊥平面PAD，由此能证明CD⊥DP．（2）连接AC交BE于N，连接MN，推导出PA∥MN，从而∠CBN=∠AEN=90°，进而△CNB≌△ANE．由此能求出k=1．（3）法一：连接CE，过点M作MF∥PE交CE于F，过A（0，1，0）作FG⊥BE于G，连接MG，则∠MGF为二面角M﹣BE﹣C的平面角，由此能示出k．
法二：以E为原点，射线EB，EA，EP分别为x正半轴，y正半轴，z正半轴建立空间直角坐标系，利用和量法能求出k．
【考点精析】认真审题，首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行)．
