题目内容
【题目】如图为四棱锥P﹣ABCD的表面展开图，四边形ABCD为矩形， 
，AD=1．已知顶点P在底面ABCD上的射影为点A，四棱锥的高为 
，则在四棱锥P﹣ABCD中，PC与平面ABCD所成角的正切值为 ．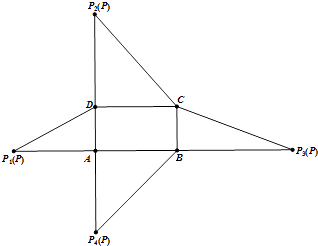 
【答案】
【解析】解：作出四棱锥的直观图如图所示：
∵顶点P在底面ABCD上的射影为点A，∴PA⊥平面ABCD，
∴∠PCA为直线PC与平面ABCD所成的角，PA= 
．
∵四边形ABCD为矩形， 
，AD=1，
∴AC= 
，
∴tan∠PCA= 
．
所以答案是： ．
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点，需要掌握已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则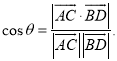
才能正确解答此题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在奥运会射箭决赛中，参赛号码为1～4号的4名射箭运动员参加射箭比赛．
（1）通过抽签将他们安排到1～4号靶位，试求恰有2名运动员所抽靶位号与其参赛号码相同的概率；
（2）记1号、2号射箭运动员射箭的环数为ξ（ξ所有取值为0，1，2，3，…，10）分别为P1 ， P2 ． 根据教练员提供的资料，其概率分布如下表：
ξ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
P1 | 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
P2 | 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
①若1，2号运动员各射箭一次，求两人中至少有一人命中9环的概率；
②判断1号、2号射箭运动员谁射箭的水平高？并说明理由．
